题目内容
2.计算:|$\frac{1}{3}$-1|=$\frac{2}{3}$.分析 首先根据有理数的减法法则,求出$\frac{1}{3}$-1的值是多少;然后根据一个负数的绝对值等于它的相反数,求出|$\frac{1}{3}$-1|的值是多少即可.
解答 解:|$\frac{1}{3}$-1|=|-$\frac{2}{3}$|=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 (1)此题主要考查了有理数的减法,要熟练掌握,解答此题的关键是要明确:①在进行减法运算时,首先弄清减数的符号;②将有理数转化为加法时,要同时改变两个符号:一是运算符号(减号变加号);二是减数的性质符号(减数变相反数).
(2)此题还考查了绝对值的含义和应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
12.已知a-$\frac{1}{a}$=1,则a2+$\frac{1}{{a}^{2}}$的值等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
10.下列计算正确的是( )
| A. | a3+a4=a7 | B. | (a3)4=a7 | C. | (-a2b3)3=a6b9 | D. | 2a4•3a5=6a9 |
14.|-5+3|=( )
| A. | -8 | B. | 8 | C. | -2 | D. | 2 |
12.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{48}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{4a+4}$ | D. | $\sqrt{14}$ |
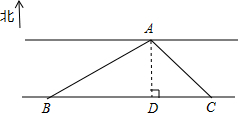 聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)
聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)