题目内容
13.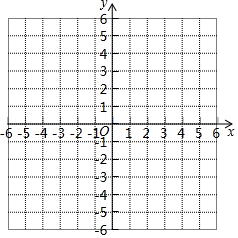 在平面直角坐标系中,点A(0,2),B(6,4).
在平面直角坐标系中,点A(0,2),B(6,4).(1)请你在x轴上标出一点C,使它到点A,B的距离之和为最小;
(2)如果在(1,0)垂直于x轴的直线可以表示为直线x=1,只限在图中,画出△ABC关于直线x=1的对称图形△A′B′C′.
分析 (1)根据平面直角坐标系找出点A、B的位置,根据轴对称确定最短路线问题,连接点B与点A关于x轴的对称点,与x轴的交点即为C点;
(2)根据网格结构找出点A、B、C关于直线x=1的对称点的位置,然后顺次连接即可.
解答 解:(1)点C如图所示;
(2)△A′B′C′如图所示.
点评 本题考查了利用轴对称变换作图,轴对称确定最短路线问题,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
4.等腰三角形周长为15cm,其中一边长为3cm,则该三角形的底边长为( )
| A. | 3cm | B. | 6cm | C. | 9cm | D. | 3cm或9cm |
1. 如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )
如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )
 如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )
如图所示,已知D、E分别是△ABC的边AB,AC上的点且DE∥BC,若S△ADE:S四边形DBCE=1:8,那么AE:EC等于( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
18.正数5的算术平方根是( )
| A. | ±$\sqrt{5}$ | B. | ±$\frac{5}{2}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
2.下列整式中,属于次数为3的单项式的是( )
| A. | 5x3y | B. | x2y+4 | C. | -8ab2 | D. | 3ab3 |
3.下列各式从左到右的变形正确的是( )
| A. | $\frac{{a}^{2}-0.2a}{{a}^{2}-0.3{a}^{3}}$=$\frac{{a}^{2}-2a}{{a}^{2}-3{a}^{3}}$ | |
| B. | -$\frac{x+1}{x-y}$=$\frac{x-1}{x-y}$ | |
| C. | $\frac{6a+1}{3}$=2a+1 | |
| D. | $\frac{x-y}{1-x}$=$\frac{y-x}{x-1}$ |
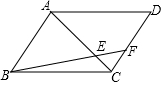 如图,在?ABCD中,点F在CD上,且CF:DF=1:2,则S△CEF:S?ABCD=1:24.
如图,在?ABCD中,点F在CD上,且CF:DF=1:2,则S△CEF:S?ABCD=1:24.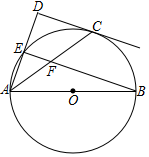 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E