题目内容
17.如图,一次函数y=-$\frac{1}{2}$x+2分别交y轴、x轴于A、B两点,抛物线y=-x2+bx+c过A、B两点,作垂直x轴的直线x=t,交x轴于H,交直线AB于M,交这个抛物线于N.(1)求这个抛物线的解析式;
(2)若M在第一象限,求当t取何值时,MN有最大值?最大值是多少?
(3)若∠ABO=∠BNH,求t的值.
分析 (1)首先求出一次函数与坐标轴交点坐标,进而代入二次函数解析式得出b,c的值即可;
(2)根据作垂直x轴的直线x=t,得出M,N的坐标,进而根据坐标性质得出即可;
(3)分别利用当t$<-\frac{1}{2}$时,-$\frac{1}{2}$≤t<4时,t≥4时,利用锐角三角函数关系求出t的值即可.
解答 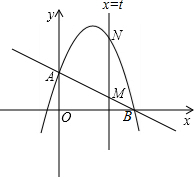 解:(1)∵一次函数y=-$\frac{1}{2}$x+2分别交y轴、x 轴于A、B两点,
解:(1)∵一次函数y=-$\frac{1}{2}$x+2分别交y轴、x 轴于A、B两点,
∴x=0时,y=2,y=0时,x=4,
∴A(0,2),B(4,0),
将x=0,y=2代入y=-x2+bx+c得c=2
将x=4,y=0,c=2代入y=-x2+bx+c,
得到b=$\frac{7}{2}$,
∴y=-x2+$\frac{7}{2}$x+2;
(2)如图:作垂直x轴的直线x=t,在第一象限交直线AB于M,
∴由题意,易得M(t,-$\frac{1}{2}$t+2),N(t,-t2+$\frac{7}{2}$t+2),
从而得到MN=-t2+$\frac{7}{2}$t+2-(-$\frac{1}{2}$t+2)=-t2+4t (0<t<4),
当t=-$\frac{b}{2a}$=2时,MN有最大值为:$\frac{4ac-{b}^{2}}{4a}$=4.
(3)∵∠ABO=∠BNH,
∴tan∠ABO=tan∠BNH
即$\frac{AO}{BO}$=$\frac{BH}{NH}$,
当-x2+$\frac{7}{2}$x+2=0时,x1=-$\frac{1}{2}$,x2=4,
①如图1,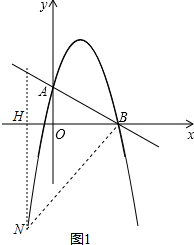
t$<-\frac{1}{2}$时,BH=4-t,NH=t2-$\frac{7}{2}$t-2,
$\frac{4-t}{{t}^{2}-\frac{7}{2}t-2}$=$\frac{2}{4}$,
解得t1=4(舍去)t2=-$\frac{5}{2}$,
∴t=-$\frac{5}{2}$,
②如图2,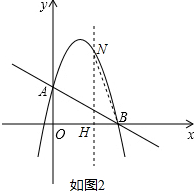
-$\frac{1}{2}$≤t<4时,BH=4-t,NH=-t2+$\frac{7}{2}$t+2,
$\frac{4-t}{-{t}^{2}+\frac{7}{2}t+2}$=$\frac{2}{4}$,
解得t1=4(舍去)t2=$\frac{3}{2}$,
∴t=$\frac{3}{2}$;
③如图3,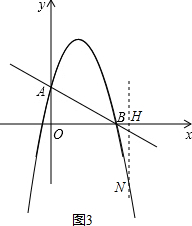
t≥4时,BH=t-4,NH=t2-$\frac{7}{2}$t-2,
$\frac{t-4}{{t}^{2}-\frac{7}{2}t-2}$=$\frac{2}{4}$,
解得t1=4(舍去)t2=$\frac{3}{2}$,
综上所述,当t=$\frac{3}{2}$或t=-$\frac{5}{2}$时,∠ABO=∠BNH.
点评 此题主要考查了一次函数与二次函数的综合应用、锐角三角函数关系等知识,根据已知分类讨论得出是解题关键.

| A. | 8% | B. | 9% | C. | 10% | D. | 11% |
 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 30°或50° |
 一个正方体的平面展开图如图,已知正方体相对两个面上的数之和相等,则a=-3,b=2.
一个正方体的平面展开图如图,已知正方体相对两个面上的数之和相等,则a=-3,b=2.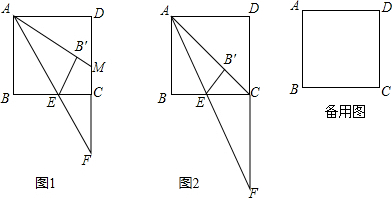
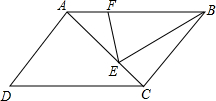 平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,求平行四边形ABCD的面积.
平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,求平行四边形ABCD的面积. 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始出发沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,当P、Q到达B、C时停止运动.求:几秒中后,P、Q间的距离为4$\sqrt{2}$cm?
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始出发沿AB向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s的速度移动,如果点P、Q分别从A、B同时出发,当P、Q到达B、C时停止运动.求:几秒中后,P、Q间的距离为4$\sqrt{2}$cm? 在平面直角坐标系xOy中,直线AB与x轴交于点A(-6,0),与y轴交于点B(0,6).
在平面直角坐标系xOy中,直线AB与x轴交于点A(-6,0),与y轴交于点B(0,6).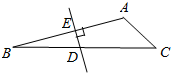 如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$.
如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$.