äãá¢áÖàï
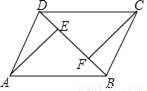
àÓë¥È˜åÖùáÝÔÅöABCDøÅȘAD=BCȘBE=DFȘAEÀëBDȘCFÀëBDȘǿæÐñøÝÞöˆEÀÂFȘúµøÊȤùáÝÔÅöAFCEòúó§ÅÅùáÝÔÅöÈÛ
êñü¯ýÃüçêÅÇÞ¯¡
üÁ¿Ääãá¢
äãá¢áÖàï
àÓë¥È˜åÖùáÝÔÅöABCDøÅȘAD=BCȘBE=DFȘAEÀëBDȘCFÀëBDȘǿæÐñøÝÞöˆEÀÂFȘúµøÊȤùáÝÔÅöAFCEòúó§ÅÅùáÝÔÅöÈÛ
