题目内容
如图,射线CE∥射线BF,射线AB∥射线CD,且AB=AC,将∠EAB绕点A顺时针旋转,∠EAB的两边分别交射线BF于点P,交射线CD于点Q.
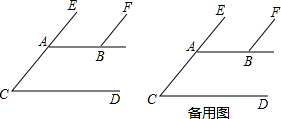
(1)画出旋转后的图形;
(2)猜想线段AP、AQ的数量关系: ;
(3)继续绕点A旋转∠EAB,使其两边分别交FB的延长线于点P,交射线CD于点Q,探索(2)中的结论是否还成立?若成立,请加以证明;若不成立,请说明理由.

(1)画出旋转后的图形;
(2)猜想线段AP、AQ的数量关系:
(3)继续绕点A旋转∠EAB,使其两边分别交FB的延长线于点P,交射线CD于点Q,探索(2)中的结论是否还成立?若成立,请加以证明;若不成立,请说明理由.
考点:作图-旋转变换,平行线的性质
专题:
分析:(1)根据将∠EAB绕点A顺时针旋转,∠EAB的两边分别交射线BF于点P,交射线CD于点Q,得出∠EAB=∠PAQ即可;
(2)根据已知首先证明四边形ACMB是平行四边形,进而得出四边形ABMC是菱形,由△ACQ∽△NMQ,得出QN•a=MN•AQ,由△NQM∽△NAB,得出QN•a=QM•AN,则MN•AQ=QM•AN,即
=
;又由△NQM∽△NPA,得出
=
,进而得出AP=AQ;
(3)利用已知可得△ACQ∽△NMQ,△NQM∽△NAB,△NQM∽△NPA,进而根据相似三角形的性质得出对应边关系,进而得出AP=AQ.
(2)根据已知首先证明四边形ACMB是平行四边形,进而得出四边形ABMC是菱形,由△ACQ∽△NMQ,得出QN•a=MN•AQ,由△NQM∽△NAB,得出QN•a=QM•AN,则MN•AQ=QM•AN,即
| MN |
| AN |
| QM |
| AQ |
| QM |
| AP |
| MN |
| AN |
(3)利用已知可得△ACQ∽△NMQ,△NQM∽△NAB,△NQM∽△NPA,进而根据相似三角形的性质得出对应边关系,进而得出AP=AQ.
解答:解:(1)如图所示:∠PAQ即为所求;

(2)AP=AQ.理由如下:
如图所示,延长PB,分别交AQ与CD于N、M点,则∠1+∠2=∠EAB,
∵∠PAQ=∠EAB,且∠2+∠3=∠PAQ,
∴∠3=∠1.
∵AB∥CD,
∴∠AQM=∠3=∠1,∠EAB=∠C.
∵BF∥EA,
∴∠APB=∠1,∠PMQ=∠C=∠EAB,
∴∠EAB=∠C=∠PAQ=∠PMQ,∠1=∠3=∠APB=∠AQM.
∵AB∥CD,AC∥BM,
∴四边形ACMB是平行四边形,
又∵AB=AC,
∴四边形ABMC是菱形.
 设AB=AC=CM=BM=a.
设AB=AC=CM=BM=a.
∵MN∥AC,
∴△ACQ∽△NMQ,
∴
=
=
,
∴QN•a=MN•AQ ①,
∵AB∥CD,
∴△NQM∽△NAB,
∴
=
=
,
∴QN•a=QM•AN ②,
比较①与②,得MN•AQ=QM•AN,
∴
=
;
∵∠NQM=∠NPA,∠QNM=∠PNA,
∴△NQM∽△NPA,
∴
=
,
∴
=
,
∴AP=AQ.
故答案为AP=AQ;
 (3)(2)中的结论还成立,理由如下:
(3)(2)中的结论还成立,理由如下:
如图所示,设FB交CD于M,FB交AQ于N.
∵AC∥FN,
∴∠CAQ=∠N,
又∵∠AQC=∠NQM,
∴△ACQ∽△NMQ,
∴
=
=
,
∴QN•a=MN•AQ,
∵AB∥CD,
∴△NQM∽△NAB,
∴
=
=
,
∴QN•a=QM•AN,
∴MN•AQ=QM•AN,
∴
=
;
∵AB∥CD,
∴∠EAB=∠C,
∵∠PAQ=∠EAB,
∴∠C=∠PAQ,
∵AC∥BN,
∴∠QMN=∠C,
∴∠PAQ=∠QMN,
又∵∠N=∠N,
∴△NQM∽△NPA,
∴
=
,
∴
=
,
∴AP=AQ.

(2)AP=AQ.理由如下:
如图所示,延长PB,分别交AQ与CD于N、M点,则∠1+∠2=∠EAB,
∵∠PAQ=∠EAB,且∠2+∠3=∠PAQ,
∴∠3=∠1.
∵AB∥CD,
∴∠AQM=∠3=∠1,∠EAB=∠C.
∵BF∥EA,
∴∠APB=∠1,∠PMQ=∠C=∠EAB,
∴∠EAB=∠C=∠PAQ=∠PMQ,∠1=∠3=∠APB=∠AQM.
∵AB∥CD,AC∥BM,
∴四边形ACMB是平行四边形,
又∵AB=AC,
∴四边形ABMC是菱形.
 设AB=AC=CM=BM=a.
设AB=AC=CM=BM=a.∵MN∥AC,
∴△ACQ∽△NMQ,
∴
| QN |
| AQ |
| NM |
| AC |
| MN |
| a |
∴QN•a=MN•AQ ①,
∵AB∥CD,
∴△NQM∽△NAB,
∴
| QN |
| AN |
| QM |
| AB |
| QM |
| a |
∴QN•a=QM•AN ②,
比较①与②,得MN•AQ=QM•AN,
∴
| MN |
| AN |
| QM |
| AQ |
∵∠NQM=∠NPA,∠QNM=∠PNA,
∴△NQM∽△NPA,
∴
| MN |
| AN |
| QM |
| AP |
∴
| QM |
| AP |
| QM |
| AQ |
∴AP=AQ.
故答案为AP=AQ;
 (3)(2)中的结论还成立,理由如下:
(3)(2)中的结论还成立,理由如下:如图所示,设FB交CD于M,FB交AQ于N.
∵AC∥FN,
∴∠CAQ=∠N,
又∵∠AQC=∠NQM,
∴△ACQ∽△NMQ,
∴
| QN |
| AQ |
| NM |
| AC |
| MN |
| a |
∴QN•a=MN•AQ,
∵AB∥CD,
∴△NQM∽△NAB,
∴
| QN |
| AN |
| QM |
| AB |
| QM |
| a |
∴QN•a=QM•AN,
∴MN•AQ=QM•AN,
∴
| MN |
| AN |
| QM |
| AQ |
∵AB∥CD,
∴∠EAB=∠C,
∵∠PAQ=∠EAB,
∴∠C=∠PAQ,
∵AC∥BN,
∴∠QMN=∠C,
∴∠PAQ=∠QMN,
又∵∠N=∠N,
∴△NQM∽△NPA,
∴
| MN |
| AN |
| QM |
| AP |
∴
| QM |
| AP |
| QM |
| AQ |
∴AP=AQ.
点评:本题考查了作图-旋转变换,菱形的判定,相似三角形的判定与性质,有一定难度.

练习册系列答案
相关题目
下列说法正确的是( )
| A、“若a是实数,则|a|>0”,该事件为必然事件 |
| B、小刚射击跳远4次,成绩为2.1,2.2,2.4,2.3,则其平均成绩为2.3 |
| C、有一组数据:3,4,5,6,6,则众数为6 |
| D、今年1至5月肉价为8元,7.2元,7.8元,8.5元,7.4元,则价格极差为1.1元 |
在正三角形、等腰梯形、矩形和圆这四种图形中,既是轴对称图形又是中心对称图形的有( )种.
| A、1 | B、2 | C、3 | D、4 |
一元二次方程(m-1)x2+x+m2-m=0的一个根为0,则m的值为( )
| A、0 | B、1 | C、1或0 | D、-1或1 |
某商店有甲乙两种笔记本,每个甲种笔记本比乙种笔记本多2元钱,且花66元购买甲种笔记本的数量与花60元购买乙种笔记本的数量相同,设每个乙种笔记本的单价是x元,根据题意,下面所列出的方程中正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM的值为( )
在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
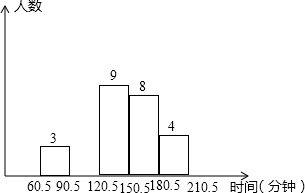 某校为了了解本校九年级学生一天中在家里做作业所用的时间,随机抽查了该校九年级的40名,并把调查所得的所有数据(时间)进行整理,分成五组,绘制成统计图(如图).
某校为了了解本校九年级学生一天中在家里做作业所用的时间,随机抽查了该校九年级的40名,并把调查所得的所有数据(时间)进行整理,分成五组,绘制成统计图(如图). 如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC于点A,若BC=6cm,则BD=
如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC于点A,若BC=6cm,则BD=