Question

1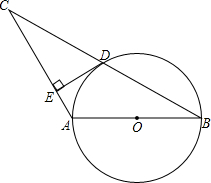．如图，⊙O的直径$AB=6，∠ABC=30°，BC=6\sqrt{3}$，D是线段BC的中点．
（1）试判断点D与⊙O的位置关系，并说明理由； 
（2）过点D作DE⊥AC，垂足为点E，求证直线DE是⊙O的切线．

Answer 1

分析 （1）设BC交⊙O于F，连接AF，求出BF和BD的长，即可得出答案；
（2）连接OD，求出OD∥AC，求出OD⊥DE，根据切线的判定得出即可．

解答 （1）解：点D与⊙O的位置关系是D在⊙O上，
理由是：
设BC交⊙O于F，连接AF，
∵AB为⊙O的直径，
∴∠AFB=90°，
∵AB=6，∠ABC=30°，
∴AF=$\frac{1}{2}$AB=3，由勾股定理得：BD=3$\sqrt{3}$，
∵BC=6$\sqrt{3}$，D为BC的中点，
∴BD=3$\sqrt{3}$，
即D、F互相重合，
∴D在⊙O上；

（2）证明：连接OD，
∵D为BC的中点，AO=BO，
∴OD∥AC，
∵DE⊥AC，
∴OD⊥DE，
∵OD为半径，
∴直线DE是⊙O的切线．

点评 本题考查了点和圆的位置关系，切线的判定，解直角三角形，圆周角定理的应用，能综合运用知识点进行推理是解此题的关键．