题目内容
根据下表中的二次函数y=ax2+bx+c（a≠0）的自变量x与函数y的对应值，可判断二次函数的图象与x轴（ ）
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -9 | -3 | -1 | -3 | … |
| A、只有一个交点 |
| B、有两个交点，且它们分别在y轴两侧 |
| C、有两个交点，且它们均在y轴同侧 |
| D、无交点 |
考点：抛物线与x轴的交点
专题：
分析：根据表中点的坐标确定函数的对称轴、顶点坐标以及开口方向，即可确定．
解答：解：函数经过点（0，-3）和（2，-3），是对称点，则对称轴是x=1，则（1，-1）是顶点．
根据点可以得到当x＜1时，y随x的增大而增大，当x＞1时，y随x的增大而减小，则函数开口向下．
故函数与x轴没有交点．
故选D．
根据点可以得到当x＜1时，y随x的增大而增大，当x＞1时，y随x的增大而减小，则函数开口向下．
故函数与x轴没有交点．
故选D．
点评：本题考查了二次函数的性质，根据点的坐标确定函数的性质是关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
已知：如图，AB=AC，∠A=36°，AB的垂直平分线交AC于D，则下列结论：①∠C=72°；②BD是∠ABC的平分线；③△ABD是等腰三角形；④△BCD是等腰三角形，其中正确的有一斜坡长10m，它的高为6m，将重物从斜坡起点推到坡上4m处停下，则停下地点的高度为（ ）
| A、2m | B、2.4m |
| C、3m | D、4m |
下列各式中正确的是（ ）
| A、|-0.5|＜0 | ||||
| B、-|-3|＞0 | ||||
C、-
| ||||
| D、|+0.4|＞|-0.4| |
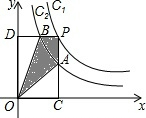如图，两个反比例函数y1=| 4 |
| x |
| 1 |
| x |
| A、2 | B、3 | C、4 | D、5 |
如果a•|a|≤0，则a为（ ）
| A、正数 | B、负数 |
| C、非负数 | D、非正数 |
已知关于x的方程（k-1）x2-2x+1=0有实数根，则k的取值范围是（ ）
| A、k≤-2 | B、k≤2 |
| C、k≥2 | D、k≤2且k≠1 |