题目内容
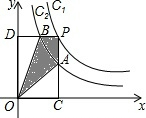 如图,两个反比例函数y1=
如图,两个反比例函数y1=| 4 |
| x |
| 1 |
| x |
| A、2 | B、3 | C、4 | D、5 |
考点:反比例函数系数k的几何意义
专题:计算题
分析:根据反比例函数系数k的几何意义得到S矩形PCOD=4,S△AOC=S△BOD=
,然后利用四边形PAOB的面积=S矩形PCOD-S△AOC-S△BOD进行计算.
| 1 |
| 2 |
解答:解:∵PC⊥x轴,PD⊥y轴,
∴S矩形PCOD=4,S△AOC=S△BOD=
×1=
,
∴四边形PAOB的面积=S矩形PCOD-S△AOC-S△BOD=4-
-
=3.
故选B.
∴S矩形PCOD=4,S△AOC=S△BOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形PAOB的面积=S矩形PCOD-S△AOC-S△BOD=4-
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了反比例函数系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
| k |
| x |

练习册系列答案
相关题目
下列各数的值为负数的是( )
| A、0×(-1) |
| B、(-1)×(-2)×(-3) |
| C、(-7)×(-2) |
| D、(-4)×(-2)2×(-10) |
下列四个函数中,当x>0时,y随x的增大而减小的是( )
| A、y=3x | ||
| B、y=x-1 | ||
C、y=-
| ||
D、y=
|
根据下表中的二次函数y=ax2+bx+c(a≠0)的自变量x与函数y的对应值,可判断二次函数的图象与x轴( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -9 | -3 | -1 | -3 | … |
| A、只有一个交点 |
| B、有两个交点,且它们分别在y轴两侧 |
| C、有两个交点,且它们均在y轴同侧 |
| D、无交点 |
|a|+|b|=|a+b|,则a,b关系是( )
| A、a,b的绝对值相等 |
| B、a,b异号 |
| C、a+b的和是非负数 |
| D、a,b同号或其中至少一个为零 |
已知|a|=3,|b|=
,且a<0<b,则a,b的值分别为( )
| 1 |
| 3 |
A、3,
| ||
B、-3,
| ||
C、-3,-
| ||
D、3,-
|
人的正常体温约是37℃,我们把体温超过正常体温的部分记作正数,那么-0.2℃表示( )
| A、体温为零下0.2℃ |
| B、体温为零上0.2℃ |
| C、体温为37.2℃ |
| D、体温为36.8℃ |
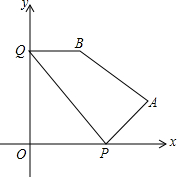 如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.
如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.