题目内容
解下列不等式:
(1)
-
≥1
(2)8(1-x)≥5(4-x)+3.
(1)
| 2x+3 |
| 2 |
| x-2 |
| 6 |
(2)8(1-x)≥5(4-x)+3.
考点:解一元一次不等式
专题:
分析:(1)先去分母,然后移项合并同类项,系数化为1,求解不等式即可;
(2)分别去括号合并同类项,系数化为1,求解不等式即可.
(2)分别去括号合并同类项,系数化为1,求解不等式即可.
解答:解:(1)去分母得:6x+9-x+2≥6,
移项合并同类项得:5x≥-5,
系数化为1得:x≥-1;
(2)去括号得:8-8x≥20-5x+3,
移项合并同类项得:-3x≥15,
系数化为1得:x≤-5.
移项合并同类项得:5x≥-5,
系数化为1得:x≥-1;
(2)去括号得:8-8x≥20-5x+3,
移项合并同类项得:-3x≥15,
系数化为1得:x≤-5.
点评:本题考查了解简单不等式的能力,解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目
根据下表中的二次函数y=ax2+bx+c(a≠0)的自变量x与函数y的对应值,可判断二次函数的图象与x轴( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -9 | -3 | -1 | -3 | … |
| A、只有一个交点 |
| B、有两个交点,且它们分别在y轴两侧 |
| C、有两个交点,且它们均在y轴同侧 |
| D、无交点 |
下列方程中是关于x的一元二次方程的是( )
| A、ax2+bx+c=0 | ||
| B、(x-1)(x+2)=1 | ||
C、x2+
| ||
| D、3x2-2xy-5y2=0 |
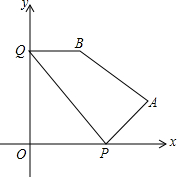 如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.
如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值. 如图,点A,B位于直线l同侧,定长为a的线段MN在直线l上滑动,问:当MN滑动到何处时,折线AMNB的长度最短?
如图,点A,B位于直线l同侧,定长为a的线段MN在直线l上滑动,问:当MN滑动到何处时,折线AMNB的长度最短?