题目内容
18.在△ABC中,CD为高,∠CAD=30°,∠CBD=45°,AC=2$\sqrt{3}$,则AB的长为3+$\sqrt{3}$或3-$\sqrt{3}$.分析 在Rt△ACD中,由三角函数的意义得到AD=$\sqrt{3}$,CD=3,由等腰三角形的性质求得BD=CD=3,即可求得答案.
解答  解:如图1,在Rt△ACD中,
解:如图1,在Rt△ACD中,
AD=AC•sin∠CAD=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,CD=AC•con∠CAD=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∵∠CBD=45°,
∴∠B=45°,
∴BD=CD=3,
∴AB=AD+BD=3+$\sqrt{3}$,
如图2,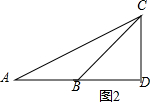 在Rt△ACD中,
在Rt△ACD中,
AD=AC•sin∠CAD=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,CD=AC•con∠CAD=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∵∠CBD=45°,
∴∠B=45°,
∴BD=CD=3,
∴AB=AD-BD=3-$\sqrt{3}$,
综上所述:AB的长为3+$\sqrt{3}$或3-$\sqrt{3}$,
故答案为:3+$\sqrt{3}$或3-$\sqrt{3}$.
点评 本题考查了解直角三角形,特殊角的三角函数,正确的画出图形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.计算(-1)2013×$(-\frac{2}{3})^{2012}$×1.52011的结果是( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
3.某种鲸鱼的体重约为1.36×105kg,关于这个近似数,下列说法正确的是( )
| A. | 它精确到百位 | B. | 它精确到0.01 | C. | 它精确到千分位 | D. | 它精确到千位 |
7.在数学课上.马小虎同学做了四道练习题.你认为他做对的题是( )
| A. | 4m2-3m2=1 | B. | 2÷$\frac{2}{5}$×$\frac{5}{2}$=2 | C. | 2x2y+3xy2=5x2y | D. | (-1)5+3=2 |
 如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,CD=8,则AE的长是( )
如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连结OC,若OC=5,CD=8,则AE的长是( )