题目内容
8. 已知:如图⊙O中,直径CD⊥弦AB于E,⊙O的半径为6cm.CE:ED=3:1,求AB的长.
已知:如图⊙O中,直径CD⊥弦AB于E,⊙O的半径为6cm.CE:ED=3:1,求AB的长.
分析 连接OA,先根据CE:ED=3:1,求得CE=9cm,DE=3cm,进而得出EO=3cm,再由勾股定理求得AE,然后根据垂径定理得出AB=2AE=6$\sqrt{3}$.
解答  解:∵⊙O的半径为6cm.
解:∵⊙O的半径为6cm.
∴CD=12cm,
∵CE:ED=3:1,
∴CE=9cm,DE=3cm,
∴EO=6-3=3cm,
连接OA,
∴AE=$\sqrt{O{A}^{2}-E{O}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∵直径CD⊥弦AB,
∴AB=2AE=6$\sqrt{3}$.
点评 本题考查的是垂径定理和勾股定理,熟练掌握着两个定理是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
17.下列说法正确的是( )
| A. | 过A、B两点的直线的长度是A、B两点之间的距离 | |
| B. | 线段AB就是A、B两点之间的距离 | |
| C. | 在A、B两点之间的所有连线中,其中最短线的长度是A、B两点的距离 | |
| D. | 乘火车从石家庄到北京要走283千米,是说石家庄与北京的距离是283千米 |
 如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠PBC=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠PBC=∠C.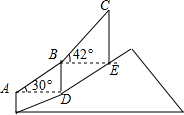 如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90). 2015年4月1日起西安市市区出租车执行新运价标准,新运价标准如公示牌所示:
2015年4月1日起西安市市区出租车执行新运价标准,新运价标准如公示牌所示: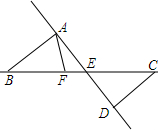 如图,直线AD,BC相交于点E,AB∥CD,F是直线BC上一点(F点与B,E,C三点不重合).
如图,直线AD,BC相交于点E,AB∥CD,F是直线BC上一点(F点与B,E,C三点不重合).