题目内容
8.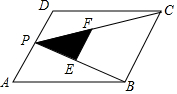 如图,P为?ABCD的边AD上的一点,E、F分别是PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=3,则S1+S2的值是( )
如图,P为?ABCD的边AD上的一点,E、F分别是PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=3,则S1+S2的值是( )| A. | 3 | B. | 6 | C. | 12 | D. | 24 |
分析 过P作PQ平行于DC,由DC与AB平行,得到PQ平行于AB,可得出四边形PQCD与ABQP都为平行四边形,进而确定出△PDC与△PCQ面积相等,△PQB与△ABP面积相等,再由EF为△BPC的中位线,利用中位线定理得到EF为BC的一半,且EF平行于BC,得出△PEF与△PBC相似,相似比为1:2,面积之比为1:4,求出△PBC的面积,而△PBC面积=△CPQ面积+△PBQ面积,即为△PDC面积+△PAB面积,即为平行四边形面积的一半,即可求出所求的面积.
解答 解:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=3,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=12.
故选:C.
点评 此题考查了平行四边形的性质,相似三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
19.观察下列图形:它们是按一定的规律排列,依照此规律第n个图形共有( )个五角星.

| A. | 1+n | B. | 1+2n | C. | 2+n | D. | 1+3n |
3.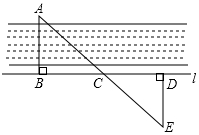 如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )
如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )
 如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )
如图,要测量河两岸相对两点A、B间的距高,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
13.下列计算正确的是( )
| A. | a4+a5=a9 | B. | a3•a3•a3=3x3 | C. | (-a3)4=a7 | D. | 2a4•3a5=6a9 |
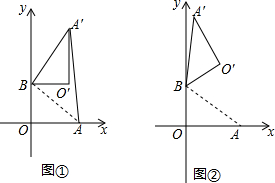
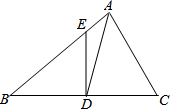 如图,在△ABC中,∠B=35°,∠C=65°,AD平分∠BAC,过点D作BC的垂线,交AB于点E,求∠ADE的度数.请完成剩下的解答过程.
如图,在△ABC中,∠B=35°,∠C=65°,AD平分∠BAC,过点D作BC的垂线,交AB于点E,求∠ADE的度数.请完成剩下的解答过程.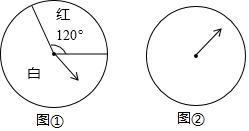
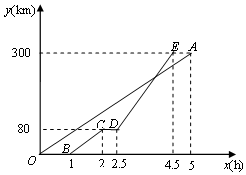 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题: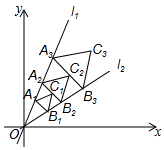 如图,点A1(1,$\sqrt{3}}$)在直线l1:y=$\sqrt{3}$x上,过点A1作A1B1⊥l1交直线l2:y=$\frac{{\sqrt{3}}}{3}$x于点B1,以A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为$\frac{\sqrt{3}}{2}$$(\frac{3}{2})^{2n-3}$.(用含n的代数式表示)
如图,点A1(1,$\sqrt{3}}$)在直线l1:y=$\sqrt{3}$x上,过点A1作A1B1⊥l1交直线l2:y=$\frac{{\sqrt{3}}}{3}$x于点B1,以A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为$\frac{\sqrt{3}}{2}$$(\frac{3}{2})^{2n-3}$.(用含n的代数式表示)