题目内容
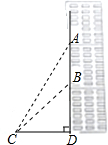 如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:利用已知得出AD=CD•tan∠ACD,BD=CD•tan∠BCD,进而利用AB=AD-BD求出即可.
解答:解:由已知可得:∠ACD=55°,∠BCD=42°,CD=20,
又∵tan∠ACD=
,tan∠BCD=
,
∴AD=CD•tan∠ACD,BD=CD•tan∠BCD,
∴AB=AD-BD=CD•tan∠ACD-CD•tan∠BCD
≈20×1.43-20×0.90
≈10.6(m)
答:AB的高度为10.6m.
又∵tan∠ACD=
| AD |
| CD |
| BD |
| CD |
∴AD=CD•tan∠ACD,BD=CD•tan∠BCD,
∴AB=AD-BD=CD•tan∠ACD-CD•tan∠BCD
≈20×1.43-20×0.90
≈10.6(m)
答:AB的高度为10.6m.
点评:此题主要考查了解直角三角形的应用,根据题意熟练应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
 如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )
如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )| A、S1>S2>S3 |
| B、S3>S2>S1 |
| C、S1=S2=S3 |
| D、S2>S3>S1 |
已知单项式3xk+mym+2与-x2y4是同类项,则k、m的值为( )
| A、k=2,m=2 |
| B、k=1,m=2 |
| C、k=2,m=-2 |
| D、k=0,m=2 |
 在四边形ABCD中,AB=AC,∠BAC=∠BDC=90°,若BD=3,DC=1,则AD=
在四边形ABCD中,AB=AC,∠BAC=∠BDC=90°,若BD=3,DC=1,则AD=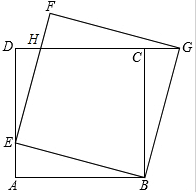 如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.
如图,正方形ABCD的边长为1,点E是AD边上的动点,从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,连接CG.