题目内容
 如图所示,∠1+∠2+∠3+∠4等于( )
如图所示,∠1+∠2+∠3+∠4等于( )| A、150° | B、240° |
| C、300° | D、330° |
考点:三角形内角和定理
专题:
分析:如图,分别在△ABC和△ADE中,利用三角形内角和定理求得,∠1+∠2=150°,∠3+∠4=150°,则易求(∠1+∠2+∠3+∠4)的度数.
解答:解:如图,

在△ABC中,∠1+∠2=180°-30°=150°.
在△ADE中,∠3+∠4=180°-30°=150°,
所以∠1+∠2+∠3+∠4=300°.
故选:C.

在△ABC中,∠1+∠2=180°-30°=150°.
在△ADE中,∠3+∠4=180°-30°=150°,
所以∠1+∠2+∠3+∠4=300°.
故选:C.
点评:本题考查了三角形内角和定理的运用,三角形的内角和定理:三角形的内角和是180度.

练习册系列答案
相关题目
已知函数y=x2-2015x+2014与x轴交点是(m,0),(n,0),则(m2-2014m+2014)(n2-2014n+2014)的值是( )
| A、2013 | B、2014 |
| C、2015 | D、2016 |
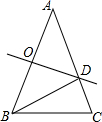 如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.则∠DBC=( )
如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.则∠DBC=( )| A、20° | B、25° |
| C、30° | D、80° |
 已知:如图,直线l:y=-x-1,一组可由平移变换得到的抛物线的顶点为B1,B2、B3、…Bn(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数),其中x1=0,x2=2,则x3=
已知:如图,直线l:y=-x-1,一组可由平移变换得到的抛物线的顶点为B1,B2、B3、…Bn(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数),其中x1=0,x2=2,则x3=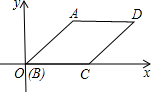 如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为
如图,?ABCD放入直角坐标系,BC在x轴上,且AB=4,BC=3,∠ABC=45°,则点D的坐标为 欣赏图,请你至少用两种方法分析图中的旋转现象.
欣赏图,请你至少用两种方法分析图中的旋转现象.