Question

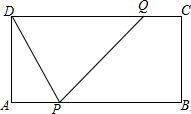在长方形ABCD中，AB=16cm，BC=6cm，点P从A点开始沿AB边向点B以3cm/s的速度移动，点Q从点C开始沿CD边向点D以2cm/s的速度移动，点P、Q从出发开始，经过几秒时，点P、Q、D组成的三角形是等腰三角形？

Answer 1

考点：等腰三角形的判定

专题：动点型

分析：设时间为ts，过P作PM⊥CD于M，过Q作QN⊥AB于N，根据四边形ABCD是矩形可知DC=AB=16cm，AD=BC=PM=QN=6cm，∠A=∠C=∠B=∠ADC=90°，故DM=AP=3tcm，CQ=BN=2tcm，再分DP=PQ，DQ=PQ及DP=DQ三种情况进行讨论即可．

解答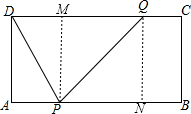：解：设时间为ts，过P作PM⊥CD于M，过Q作QN⊥AB于N，
∵四边形ABCD是矩形，
∴DC=AB=16cm，AD=BC=PM=QN=6cm，∠A=∠C=∠B=∠ADC=90°，
则DM=AP=3tcm，CQ=BN=2tcm，
分为三种情况：①当DP=PQ时，则DM=MQ=3tcm，
∵3t+3t+2t=16，
解得：t=2；
②当DQ=PQ时，在Rt△PNQ中，由勾股定理得：（16-2t）²=6²+（16-3t-2t）²，
7t²-32t+12=0，
解得：t=

32±4 43

14

=

16±2 43

7

，
∵t=

16+2 43

7

＞

16

3

（舍去），
∴t=

16-2 43

7

；
③当DP=DQ时，在Rt△DAP中，由勾股定理得：（16-2t）²=6²+（3t）²，
即5t²+64t-220=0，
解得t=

-64±12 59

10

=

-32±6 59

5

，
∵

-32-6 59

5

＜0，
∴t=

-32+6 59

5

．
答：经过2秒、

16-2 43

7

秒或

-32+6 59

5

秒时，点P、Q、D组成的三角形是等腰三角形．

点评：本题考查的是等腰三角形的判定，在解答此题时要注意进行分类讨论，不要漏解．