题目内容
利用“剪、拼”的方法将任意一块三角形纸片变成一个与原三角形面积相等的平行四边形纸片，请说明你的做法，并证明你的做法的合理性．考点：图形的剪拼,平行四边形的性质
专题：
分析：利用三角形中位线的性质以及旋转的性质，将△EFC旋转180°到△BFD位置，进而利用平行四边形的判定得出即可．
解答：
解：如图所示：四边形ABDE即为所求．
沿AC的中点E，以及BC的中点F，减掉△EFC，再将△EFC旋转180°到△BFD位置，
∵AE=EC，EC=BD，
∴BD=EC=AE，
∵∠A=∠CEF，∠BDF=∠CEF，
∴∠D=∠CEF，
∴BD∥AC，
∴四边形ABDE是平行四边形．
解：如图所示：四边形ABDE即为所求．沿AC的中点E，以及BC的中点F，减掉△EFC，再将△EFC旋转180°到△BFD位置，
∵AE=EC，EC=BD，
∴BD=EC=AE，
∵∠A=∠CEF，∠BDF=∠CEF，
∴∠D=∠CEF，
∴BD∥AC，
∴四边形ABDE是平行四边形．
点评：此题主要考查了图形的剪拼以及平行四边形的判定以及旋转的性质等，利用三角形中位线性质得出是解题关键．
练习册系列答案
相关题目
如图所示的物体是由四个相同的小长方体堆砌而成的，那么这个物体的左视图是（ ）
一个三角形的三个内角分别为α，α-1°，α+1°（α＞1°），则这个三角形三个内角的度数分别为（ ）
| A、44°，45°，91° |
| B、49°，59°，69° |
| C、59°，60°，61° |
| D、30°，60°，90° |
如果
•
=
，那么x应满足的条件是（ ）
| x |
| x-5 |
| x(x-5) |
| A、x≥0 | B、x≤0 |
| C、0≤x≤5 | D、x≥5 |
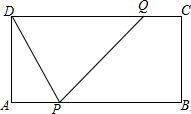在长方形ABCD中，AB=16cm，BC=6cm，点P从A点开始沿AB边向点B以3cm/s的速度移动，点Q从点C开始沿CD边向点D以2cm/s的速度移动，点P、Q从出发开始，经过几秒时，点P、Q、D组成的三角形是等腰三角形？
如图所示，有4个动点P，Q，E，F分别从正方形ABCD的4个顶点出发，分别沿着AB，BC，CD，DA以同样的速度向B，C，D，A各点移动．
如图，已知△AOB∽△DOC，OA=2，AD=9，OB=5，DC=12．求AB，OC的长．