题目内容
2.一木杆在离地面6米处折断,木杆顶端落在离木杆底端8米处,木杆折断前的总长度是( )米.| A. | 10米 | B. | 14米 | C. | 16米 | D. | 20米 |
分析 先根据木杆离地面部分、折断部分及地面正好构成直角三角形利用勾股定理求出折断部分的长,进而可得出结论.
解答  解:∵木杆离地面部分、折断部分及地面正好构成直角三角形,即△ABC是直角三角形,
解:∵木杆离地面部分、折断部分及地面正好构成直角三角形,即△ABC是直角三角形,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$,
∵AB=6米,AC=8米,
∴BC=$\sqrt{{6}^{2}+{8}^{2}}$=10(米),
∴木杆的高度=AB+BC=6+10=16(米).
故选:C.
点评 此题考查了勾股定理的应用,主要考查学生对勾股定理在实际生活中的运用能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
17.下列各式中,不是同类项的是( )
| A. | $\frac{1}{2}$ab和5ba | B. | a3和53 | C. | $\frac{xy}{5}$和52xy | D. | 102和$\frac{1}{10}$ |
7.如图图形是由一些小正方形和实心圆按一定规律排列而成的,如图所示,按此规律排列下去,第20个图形中有( )个实心圆.


| A. | 38 | B. | 40 | C. | 42 | D. | 44 |
14.已知直角三角形的两条直角边分别是3和4,则它斜边上的中线长为( )
| A. | 2.4 | B. | 2.5 | C. | 3 | D. | 5 |
11.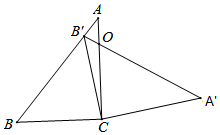 如图,在△ABC中,∠ACB=90°,∠B=50°,将它绕点C沿顺时针方向旋转后得到△A′B′C′.若点B′恰好落在线段AB上,则旋转角的度数是( )
如图,在△ABC中,∠ACB=90°,∠B=50°,将它绕点C沿顺时针方向旋转后得到△A′B′C′.若点B′恰好落在线段AB上,则旋转角的度数是( )
 如图,在△ABC中,∠ACB=90°,∠B=50°,将它绕点C沿顺时针方向旋转后得到△A′B′C′.若点B′恰好落在线段AB上,则旋转角的度数是( )
如图,在△ABC中,∠ACB=90°,∠B=50°,将它绕点C沿顺时针方向旋转后得到△A′B′C′.若点B′恰好落在线段AB上,则旋转角的度数是( )| A. | 40° | B. | 50° | C. | 70° | D. | 80° |
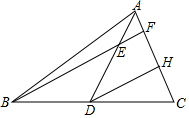 如图,AD为△ABC的中线,AE=$\frac{1}{3}$AD,BE交AC于点F,DH∥BF,则$\frac{AF}{CH}$=$\frac{1}{2}$.
如图,AD为△ABC的中线,AE=$\frac{1}{3}$AD,BE交AC于点F,DH∥BF,则$\frac{AF}{CH}$=$\frac{1}{2}$.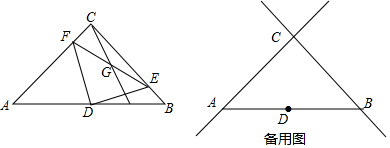
 如图,小张和小刘身高相同,在灯光下,小张的影子比小刘的影子长,这说明小张比小刘距离灯光远.
如图,小张和小刘身高相同,在灯光下,小张的影子比小刘的影子长,这说明小张比小刘距离灯光远.