题目内容
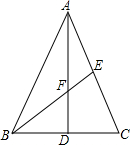 如图,△ABC中,AB=AC,AD⊥BC,D为垂足,E为AC中点,BE交AD于F.
如图,△ABC中,AB=AC,AD⊥BC,D为垂足,E为AC中点,BE交AD于F. (1)求证:
| DF |
| AF |
| EF |
| BF |
(2)若四边形CDFE的面积为8,求△ABC的面积.
考点:相似三角形的判定与性质
专题:
分析:(1)证明DE∥AB,得到△DEF∽△ABF,即可解决问题.
(2)证明S△ABF=4S△DEF(设为μ),S△ABC=4S△CDE,列出有关面积λ、μ的方程组,解方程组即可解决问题.
(2)证明S△ABF=4S△DEF(设为μ),S△ABC=4S△CDE,列出有关面积λ、μ的方程组,解方程组即可解决问题.
解答: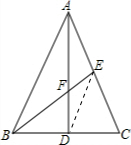 解:(1)∵AB=AC,AD⊥BC,
解:(1)∵AB=AC,AD⊥BC,
∴BD=CD;而AE=CE,
∴DE∥AB,且DE=
AB;
∴△DEF∽△ABF,
∴
=
.
(2)∵DE∥AB,
∴△ADE与△BDE的面积相等,
∴△AEF与△BDF的面积也相等,设为λ;
∵△DEF∽△ABF,
∴
=(
)2=
;
∴S△ABF=4S△DEF(设为μ),
∴四边形ABDE的面积=2λ+5μ;
同理可证:S△ABC=4S△CDE,
∴S△CDE=
(2λ+5μ);
∵S四边形CDFE=8,
∴μ+
(2λ+5μ)=8①;
∵BD=CD,
∴S△ABD=S△ACD,而S△BDF=S△AEF,
∴S△ABF=S四边形DCEF=8,
即4μ=8②,
联立①②并解得:λ=4,μ=4,
∴△ABC的面积=4μ+2λ+8=32.
 解:(1)∵AB=AC,AD⊥BC,
解:(1)∵AB=AC,AD⊥BC,∴BD=CD;而AE=CE,
∴DE∥AB,且DE=
| 1 |
| 2 |
∴△DEF∽△ABF,
∴
| DF |
| AF |
| EF |
| BF |
(2)∵DE∥AB,
∴△ADE与△BDE的面积相等,
∴△AEF与△BDF的面积也相等,设为λ;
∵△DEF∽△ABF,
∴
| S△DEF |
| S△ABF |
| DE |
| AB |
| 1 |
| 4 |
∴S△ABF=4S△DEF(设为μ),
∴四边形ABDE的面积=2λ+5μ;
同理可证:S△ABC=4S△CDE,
∴S△CDE=
| 1 |
| 3 |
∵S四边形CDFE=8,
∴μ+
| 1 |
| 3 |
∵BD=CD,
∴S△ABD=S△ACD,而S△BDF=S△AEF,
∴S△ABF=S四边形DCEF=8,
即4μ=8②,
联立①②并解得:λ=4,μ=4,
∴△ABC的面积=4μ+2λ+8=32.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断;对综合的分析问题解决问题的能力、运算求解能力均提出了一定的要求.

练习册系列答案
相关题目
反比例函数y=
(k为常数,k≠0)的自变量x的取值范围是( )
| k |
| x |
| A、x>0 | B、x≠0 |
| C、x≥0 | D、k≠0 |
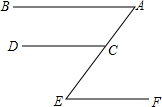 如图,CD∥EF,∠ECD=∠A,则EF∥AB,说明理由如下:
如图,CD∥EF,∠ECD=∠A,则EF∥AB,说明理由如下: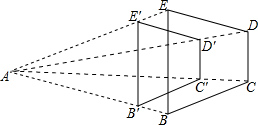 如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE. 在直角△ABC中,AB=AC,∠BAC=90°,D为AC的中点,过点A作AE⊥BD于E,交BC于点F,求证:BF=2CF.
在直角△ABC中,AB=AC,∠BAC=90°,D为AC的中点,过点A作AE⊥BD于E,交BC于点F,求证:BF=2CF. 如图,
如图,