题目内容
在Rt△ABC中,∠C=90°,cosA=
,c=20.试解这个直角三角形.
| 3 |
| 5 |
考点:解直角三角形
专题:
分析:根据已知条件和三角函数公式,可求出各角的度数和直角边的长度.
解答:解:∵∠C=90°,cosA=
,
∴b=c•cosA=20×
=12,
∴a=
=16,
∵cosA=
=0.6,
∴∠A≈53°8′,
∴∠B=90°-∠A≈90°-53°8′=36°52′.
| 3 |
| 5 |
∴b=c•cosA=20×
| 3 |
| 5 |
∴a=
| 202-122 |
∵cosA=
| 3 |
| 5 |
∴∠A≈53°8′,
∴∠B=90°-∠A≈90°-53°8′=36°52′.
点评:此题主要考查了解直角三角形,在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解直角三角形常常用到以下关系:
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:sinA=∠A的对边:斜边=a:c,cosA=∠A的邻边:斜边=b:c,tanA=∠A的对边:∠A的邻边=a:b.(a,b,c分别是∠A、∠B、∠C的对边).
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:sinA=∠A的对边:斜边=a:c,cosA=∠A的邻边:斜边=b:c,tanA=∠A的对边:∠A的邻边=a:b.(a,b,c分别是∠A、∠B、∠C的对边).

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
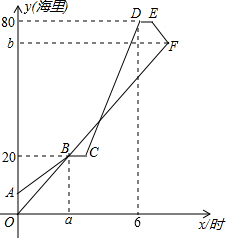 在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.
在距离港口80海里处,有一艘渔船发出求救信息,甲、乙两艘救援船同时接到救援任务,甲船立即出发,乙船因需要等候救援家属,在甲救援船驶离港口5海里时才出发.乙船以10海里/小时的速度匀速行驶,甲船途中因故障维修停船1小时,然后提高速度匀速行驶,到达目的地救援1小时后原路匀速返回与乙船相遇,甲船返回时的速度与提高后的速度相同,图中折线AB-BC-CD-DE-EF,线段OF分别表示甲、乙两船与港口的距离y(海里)与乙船出发时间x(时)之间的图象.
 如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6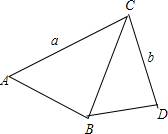 如图所示,已知AB⊥BC,BD⊥CD,AC=a,BC=b.试猜想BD与a,b之间满足怎样的关系时这两个三角形相似?并说明理由.
如图所示,已知AB⊥BC,BD⊥CD,AC=a,BC=b.试猜想BD与a,b之间满足怎样的关系时这两个三角形相似?并说明理由.