题目内容
17. 如图,在△ABC中,过顶点A的直线DE∥BC,∠ABC、∠ACB的平分线分别交DE于点E、D,若AC=3,AB=4,则DE的长为( )
如图,在△ABC中,过顶点A的直线DE∥BC,∠ABC、∠ACB的平分线分别交DE于点E、D,若AC=3,AB=4,则DE的长为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 BE为∠ABC的角平分线,∠EBC=∠ABE,CD为∠ACB的角平分线,则∠ACD=∠DCB,因为BC∥DE,根据平行线的性质,内错角相等,可得出AD=AC,AB=AE,所以DE=AD+AE=AB+AC,从而可求出DE的长度.
解答 解:由分析得:∠EBC=∠ABE,∠ACD=∠DCB;
根据平行线的性质得:∠DCB=∠CDE,∠EBC=∠BED;
所以∠ADC=∠ACD,∠ABE=∠AEB,则AD=AC,AB=AE;
所以DE=AD+AE=AB+AC=3+4=7;
故选B.
点评 本题综合考查了勾股定理、平行线的性质以及等腰三角形的判定与性质.根据勾股定理求得AB是本题的重点.

练习册系列答案
相关题目
7.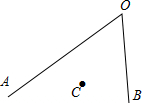 某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
 某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
某班举行文艺晚会,桌子摆成两条直线(OA、OB),OA桌面上摆满了橘子,OB桌面摆满了糖果,坐在C处的小明先拿橘子再拿糖果,然后回到座位,请你帮助他设计路线,使其行走的总路程最短.(保留作图痕迹)
8.绝对值不大于5.1的整数有( )
| A. | 11个 | B. | 12个 | C. | 22个 | D. | 23个 |
12.已知P1(-3,y1)、P2(-2,y2)是二次函数y=-2(x+1)2+1图象上的两个点,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1≤y2 | C. | y1>y2 | D. | 无法确定 |
2.下列说法中正确的是( )
| A. | 轴对称图形只有一条对称轴 | |
| B. | 两个三角形关于某直线对称,不一定全等 | |
| C. | 两个全等三角形一定成轴对称 | |
| D. | 直线MN垂直平分线段AB,则直线MN是线段AB的对称轴 |
7. 实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
 实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a、b在数轴上的位置如图所示,那么化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )| A. | 2a-b | B. | b | C. | -b | D. | -2a+b |
