题目内容
3.已知抛物线y=$\frac{1}{2}$x2+mx-2m-2(m≥0)与x轴交于A、B两点,点A在点B的左边,与y轴交于点C(1)当m=1时,求点A和点B的坐标
(2)抛物线上有一点D(-1,n),若△ACD的面积为5,求m的值
(3)P为抛物线上A、B之间一点(不包括A、B),PM⊥x轴于点M,求$\frac{AM•BM}{PM}$的值.
分析 (1)当m=1时,抛物线解析式为y=$\frac{1}{2}$x2+x-4.然后解方程$\frac{1}{2}$x2+x-4=0可得A、B的坐标;
(2)过点D作DE⊥AB于点E,交AC于点F,如图,解方程$\frac{1}{2}$x2+mx-2m-2=0得x1=2,x2=-2m-2,则A为(-2m-2,0),B(2,0),易得C(0,-2m-2),所以OA=OC=2m+2,则∠OAC=45°.利用D(-1,n)得到OE=1,AE=EF=2m+1.n=-3m-$\frac{3}{2}$,再计算出DF=m+$\frac{1}{2}$,利用三角形面积公式得到$\frac{1}{2}$(m+$\frac{1}{2}$)(2m+2)=5.解方程得到m1=$\frac{3}{2}$,m2=-3,最后利用m≥0得到m=$\frac{3}{2}$;
(3)由(2)得点A(-2m-2,0),B(2,0).设点P的坐标为(p,q).则AM=p+2m+2,BM=2-p,
AM•BM=-p2-2mp+4m+4,PM=-q.再利用点P在抛物线上得到q=$\frac{1}{2}$p2+mp-2m-2,所以AM•BM=2 PM,从而得到$\frac{AM•BM}{PM}$的值.
解答 解:(1)当m=1时,抛物线解析式为y=$\frac{1}{2}$x2+x-4.
当y=0时,$\frac{1}{2}$x2+x-4=0,解得x1=-4,x2=2.
∴A(-4,0),B(2,0);
(2)过点D作DE⊥AB于点E,交AC于点F,如图,
当y=0时,$\frac{1}{2}$x2+mx-2m-2=0,则(x-2)(x+2m+2)=0,
解得x1=2,x2=-2m-2,
∴点A的坐标为(-2m-2,0),B(2,0),
当x=0时,y=-2m-2,则C(0,-2m-2),
∴OA=OC=2m+2,
∴∠OAC=45°.
∵D(-1,n),
∴OE=1,
∴AE=EF=2m+1.
当x=-1时,n=$\frac{1}{2}$-m-2m-2=-3m-$\frac{3}{2}$,
∴DE=3m+$\frac{3}{2}$,
∴DF=3m+$\frac{3}{2}$-(2m+1)=m+$\frac{1}{2}$,
又∵S△ACD=$\frac{1}{2}$DF•AO.
∴$\frac{1}{2}$(m+$\frac{1}{2}$)(2m+2)=5.
2m2+3m-9=0,解得m1=$\frac{3}{2}$,m2=-3.
∵m≥0,
∴m=$\frac{3}{2}$;
(3)点A的坐标为(-2m-2,0),点B的坐标为(2,0).
设点P的坐标为(p,q).则AM=p+2m+2,BM=2-p,
AM•BM=(p+2m+2)( 2-p)=-p2-2mp+4m+4,
PM=-q.
因为点P在抛物线上,
所以q=$\frac{1}{2}$p2+mp-2m-2.
所以AM•BM=2 PM.
即$\frac{AM•BM}{PM}$=2.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

 名校课堂系列答案
名校课堂系列答案有这样一个问题:关于x 的一元二次方程a x2+bx+c=0(a>0)有两个不相等的且非零的实数根.探究a,b,c满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:
①设一元二次方程ax2+bx+c=0(a>0)对应的二次函数为y=ax2+bx+c(a>0);
②借助二次函数图象,可以得到相应的一元二次中a,b,c满足的条件,列表如下:
方程根的几何意义:请将(2)补充完整
| 方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
| 方程有两个 不相等的负实根 | 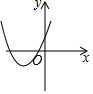 | $\left\{\begin{array}{l}a>0\\△={b^2}-4ac>0\\-\frac{b}{2a}<0\\ c>0.\end{array}\right.$ |
| 方程有一个负实根,一个正实根 | 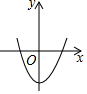 | $\left\{\begin{array}{l}a>0\\ c<0.\end{array}\right.$ |
| 方程有两个 不相等的正实根 | 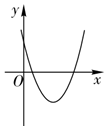 | $\left\{\begin{array}{l}a>0\\△={b^2}-4ac>0\\-\frac{b}{2a}>0\\ c>0.\end{array}\right.$ |
(2)若一元二次方程mx2-(2m+3)x-4m=0有一个负实根,一个正实根,且负实根大于-1,求实数m的取值范围.
| A. |  | B. |  | C. |  | D. |  |
 如图所示,数轴上点A、B对应的有理数分别为a、b,下列说法正确的是( )
如图所示,数轴上点A、B对应的有理数分别为a、b,下列说法正确的是( )| A. | ab>0 | B. | a+b>0 | C. | |a|-|b|<0 | D. | a-b<0 |
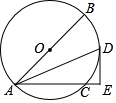 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.