题目内容
(1)如图1,平面内有一等腰直角三角板ABC(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F,试证明线段AF,BF,CE之间的数量关系为AF+BF=2CE 。
(提示:过点C做BF的垂线,利用三角形全等证明。)
(2)若三角板绕点A顺时针旋转至图2的位置,其他条件不变,试猜想线段AF、BF、CE之间的数量关系,并证明你的猜想。
(3) 若三角板绕点A顺时针旋转至图3的位置,其他条件不变,则线段AF、BF、CE之间的数量关系为
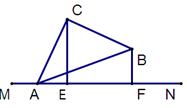
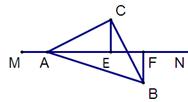
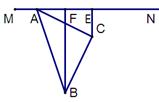
第22题图1 第22题图2 第22题图3
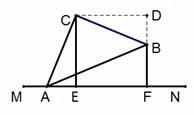
(1)证明:过点C 做CD⊥BF,交FB的延长线于点D
做CD⊥BF,交FB的延长线于点D
∵CE⊥MN,CD⊥BF
∴∠CEA=∠D=90°
∵CE⊥MN,CD⊥BF,BF⊥MN
∴四边形CEFD为矩形
∴∠ECD=90°
 又∵∠ACB=90°
又∵∠ACB=90°
∴∠ACB-∠ECB=∠ECD-∠ECB
即∠ACE=∠BCD
又∵△ABC为等腰直角三角形
∴AC=BC
∴△ACE≌△BCD(AAS)
∴AE=BD,CE=CD
又∵四边形CEFD为矩形
∴四边形CEFD为正方形
∴CE=EF=DF=CD
∴AF+BF=AE+EF+BF
=BD+EF+BF
=DF+EF
=2CE
(2)AF-BF=2CE
过程同(1)理,略
(3)BF-AF=2CE

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
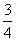 ,BC=5;
,BC=5;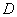 是直线
是直线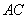 上的一个动点,当
上的一个动点,当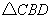 为等腰三角形时,
为等腰三角形时, 求CD的长(5分).
求CD的长(5分).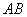 上是否存在点
上是否存在点 ,使OA∥DE、且以点
,使OA∥DE、且以点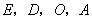 为顶点的
为顶点的 四边形是平行四边形?如果存在,直接写出
四边形是平行四边形?如果存在,直接写出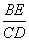 的值;如果不存在,请说明理由.(5分)
的值;如果不存在,请说明理由.(5分)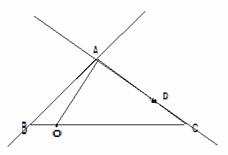



 B.2
B.2 的平方根是( )
的平方根是( ) D、±
D、±