题目内容
【题目】已知:正方形![]() 与正方形
与正方形![]() 共顶点
共顶点![]() .
.
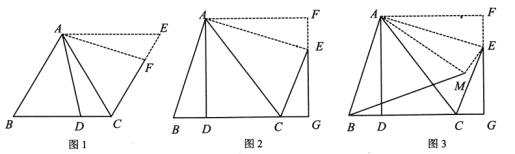
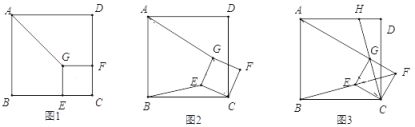
(1)探究:如图,点![]() 在正方形
在正方形![]() 的边
的边![]() 上,点
上,点![]() 在正方形
在正方形![]() 的边
的边![]() 上,连接
上,连接![]() .求证:
.求证:![]() ;
;
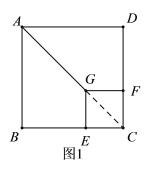
(2)拓展:将如图中正方形![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角
角![]() ,如图所示,试探究线段
,如图所示,试探究线段![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
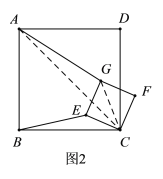
(3)运用:正方形![]() 在旋转过程中,当
在旋转过程中,当![]() ,
,![]() ,
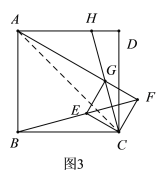
,![]() 三点在一条直线上时,如图所示,延长
三点在一条直线上时,如图所示,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() ,GH=2
,GH=2![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)线段![]() 与
与![]() 之间的数量关系为
之间的数量关系为![]() ;理由见解析;(3)
;理由见解析;(3)![]() .
.
【解析】
(1)连接![]() ,由正方形性质知∠CEG=∠B=90°、∠ECG=45°,据此可得
,由正方形性质知∠CEG=∠B=90°、∠ECG=45°,据此可得![]() 、GE∥AB,利用平行线分线段成比例定理可得;
、GE∥AB,利用平行线分线段成比例定理可得;
(2)连接![]() ,
,![]() ,只需证△ACG∽△BCE即可得;
,只需证△ACG∽△BCE即可得;
(3)证△AHG∽△CHA得![]() ,设BC=CD=AD=a,知AC=
,设BC=CD=AD=a,知AC=![]() a,由
a,由![]() 得AH=
得AH=![]() a、DH=
a、DH=![]() a、CH=
a、CH=![]() a,由
a,由![]() 可得a的值.
可得a的值.
(1)连接![]()
∵四边形![]() 是正方形,∴
是正方形,∴![]() ,
,![]() ,
,![]()
∵四边形![]() 是正方形,∴
是正方形,∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() 三点在一条直线上
三点在一条直线上
∵![]() ,
,![]() ∴
∴![]()
∴![]() ∴
∴![]()
(2)连接![]() ,
,![]() ,
,
∵![]() ∴
∴![]() ,
,
在![]() 和
和![]() 中,
中,
![]() 、
、![]() ,
,
∴![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴线段![]() 与
与![]() 之间的数量关系为
之间的数量关系为![]() ;
;
(3)由(2)可知![]()
∵![]() ,点
,点![]() 、
、![]() 、
、![]() 三点共线, ∴
三点共线, ∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∴![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
则由![]() 得
得![]() , ∴
, ∴![]() ,
,
则![]() ,
,![]() , ∴
, ∴![]() 得
得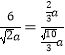 ,
,
解得:![]() ,即
,即![]() ,
,

练习册系列答案
相关题目