题目内容
【题目】阅读材料：我们知道，在四边形ABCD中，当对角线
，若
，
时，
（1）则四边形ABCD的面积为 ；
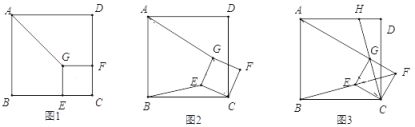
小凯遇到一个问题：如图1，在四边形ABCD中，对角线AC、BD相交于点O，，，
，求四边形ABCD的面积。
小凯发现，如图2分别过点A、C作直线BD的垂线，垂足分别为点E，F，设AO为m，通过计算
与
的面积和使问题得以解决。
请回答：
（2）的面积为 （用含m的式子表示）
（3）求四边形ABCD的面积。
参考小凯思考问题的方法，解决问题：如图3，在四边形ABCD中，对角线AC、BD相交于点O，
，
，
（
），则四边形ABCD的面积为 （用含a，b，
的式子表示）
【答案】（1）12；（2）
；（3）
；解决问题：
.
【解析】
(1) 设AC与BD的垂足为O，根据三角形的面积公式得到S△ABC=
ACOC，S△ADC=ACOD，两式相加得到S四边形ABCD=S△ABC+S△ADC=ACOC+ACOD=ACBD，然后把AC=4，BD=6代入计算即可;
(2)首先得出AE的长，再利用三角形的面积公式求出即可；
(3)根据直角三角形的性质可得AE=m，再根据三角形的面积公式可得S△ABD=BDAE＝
m，同理再表示CF= (4m)，然后再表示△BCD的面积，再求两个三角形的面积和可得答案；解决问题：方法类似.
(1) 设AC与BD的垂足为O，如图所示：
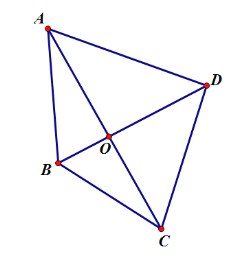
∴S△ABC=ACOB，S△ADC=ACOD，
∴S四边形ABCD=S△ABC+S△ADC=ACOB+ACOD=ACBD，
而AC=4，BD=6，
∴S四边形ABCD=46=12．
故答案是：12．
(2)∵AO=m，∠AOB=30°，
∴AE=m，
∴△ABD的面积为：
×m×6=m；
故答案为：m；
(3)
,
∵
，
,
∴
,
∴
,
同理：
,
∴
,
∴
;
解决问题：分别过点A、C作直线BD的垂线，垂足分别为点E，F，设
,
∵，
,
∴
,
∴
,
同理：
,
∴
,
∴
.
