题目内容
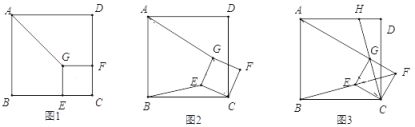
【题目】(探索发现)
如图,![]() 是等边三角形,点
是等边三角形,点![]() 为
为![]() 边上一个动点,将
边上一个动点,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .小明在探索这个问题时发现四边形
.小明在探索这个问题时发现四边形![]() 是菱形.
是菱形.
小明是这样想的:
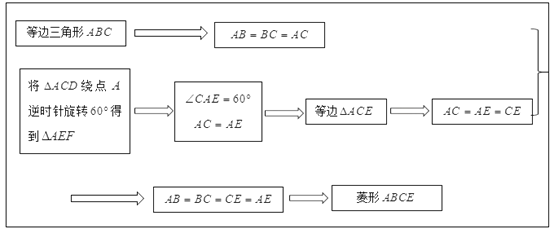
(1)请参考小明的思路写出证明过程;
(2)直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系:______________;
之间的数量关系:______________;
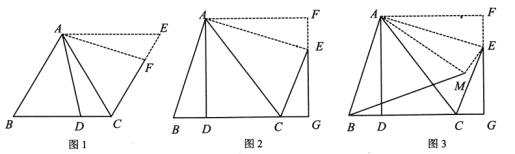
(理解运用)
如图,在![]() 中,
中,![]() 于点
于点![]() .将
.将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,延长
,延长![]() 与
与![]() ,交于点
,交于点![]() .
.
(3)判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(拓展迁移)
(4)在(3)的前提下,如图,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() ;(3)四边形
;(3)四边形![]() 是正方形;(4)
是正方形;(4)![]()
【解析】
(1)根据旋转得:△ACE是等边三角形,可得:AB=BC=CE=AE,则四边形ABCE是菱形;
(2)先证明C、F、E在同一直线上,再证明△BAD≌△CAF(SAS),则∠ADB=∠AFC,BD=CF,可得AC=CF+CD;
(3)先根据∠ADC=∠DAF=∠F=90°,证明得四边形ADGF是矩形,由邻边相等可得四边形ADGF是正方形;
(4)证明△BAM≌△EAD(SAS),根据BM=DE及勾股定理可得结论.
(1)证明:∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴![]() ,
,![]() .
.
∴![]() 是等边三角形.
是等边三角形.
∴![]() .
.
∴![]() .
.
∴四边形![]() 是菱形.
是菱形.
(2)线段![]() ,
,![]() ,
,![]() 之间的数量关系:
之间的数量关系:![]() .
.
(3)四边形![]() 是正方形.理由如下:
是正方形.理由如下:
∵![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴四边形![]() 是矩形.
是矩形.
∵![]() ,
,
∴四边形![]() 是正方形.
是正方形.
(4)如图,连接![]() .
.
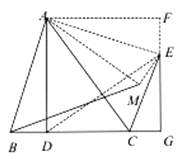
∵四边形![]() 是正方形,
是正方形,
∴![]() .
.
∵![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.
∵将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,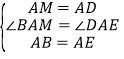 ,
,
∴![]() .
.
∴![]() .
.

练习册系列答案
相关题目