题目内容
6.若关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,则k的取值范围在数轴上表示正确的是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据一元二次方程的定义结合根的判别式,即可得出关于k的一元一次不等式组,解之即可得出k的取值范围,将其表示在数轴上即可得出结论.
解答 解:∵关于x的一元二次方程(k+1)x2+2(k+1)x+k-2=0有实数根,
∴$\left\{\begin{array}{l}{k+1≠0}\\{△=[2(k+1)]^{2}-4(k+1)(k-2)≥0}\end{array}\right.$,
解得:k>-1.
故选A.
点评 本题考查了根的判别式、一元二次方程的定义以及在数轴上表示不等式的解集,根据一元二次方程的定义结合根的判别式,找出关于k的一元一次不等式组是解题的关键.

练习册系列答案
相关题目
16.对多项式x2-2x+1因式分解,结果正确的是( )
| A. | (x+1)2 | B. | (x+1)(x-1) | C. | (x-1)2 | D. | (x+1)(x-2) |
1.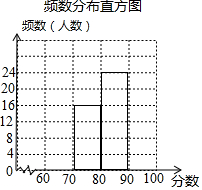 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
频数分布表
请解答下列问题:
(1)完成频数分布表,a=4,b=4.
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.频数分布表
| 分数段 | 频数(人数) |
| 60≤x<70 | a |
| 70≤x<80 | 16 |
| 80≤x<90 | 24 |
| 90≤x<100 | b |
(1)完成频数分布表,a=4,b=4.
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
5.一中学有学生3000名,2016年母亲节,晓彤为了调查本校大约有多少学生知道自己母亲的生日,随机调查了200名学生,有20名同学不知道自己母亲生日,关于这个数据收集和处理的问题,下列说法错误的是( )
| A. | 个体是该校每一位学生 | |
| B. | 本校约有300名学生不知道自己母亲的生日 | |
| C. | 调查的方式是抽样调查 | |
| D. | 样本是随机调查的200名学生是否知道自己母亲的生日 |
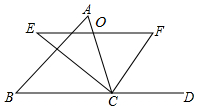 如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.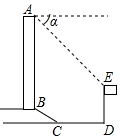 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45) 如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).
如图,矩形OABC的边OA,OC分别在坐标轴上,OA=4,OC=8,把△ABC沿着AC折叠.点B落在点B′处,AB′交y轴于点D,则点D的坐标是(0,3).