题目内容
14．化简：（a+1-$\frac{3}{a-1}$）÷$\frac{a-2}{2a-2}$，然后给a从1，2，3中选取一个合适的数代入求值．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值．
解答 解：原式=$\frac{（a+1）（a-1）-3}{a-1}$•$\frac{2（a-1）}{a-2}$=$\frac{（a+2）（a-2）}{a-1}$•$\frac{2（a-1）}{a-2}$=2（a+2）=2a+4，
当a=3时，原式=6+4=10．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
4．
如图，正方形网格中，每个小正方形的边长是1个单位长度，以点C为位似中心，在网格中画△A1B1C1，使△A1B1C1与△ABC位似，且△A1B1C1与△ABC的位似比为2：1，则点B1的坐标可以为（ ）
如图，正方形网格中，每个小正方形的边长是1个单位长度，以点C为位似中心，在网格中画△A1B1C1，使△A1B1C1与△ABC位似，且△A1B1C1与△ABC的位似比为2：1，则点B1的坐标可以为（ ）| A． | （3，-2） | B． | （4，0） | C． | （5，-1） | D． | （5，0） |
5．下列命题的逆命题是假命题的是（ ）
| A． | 对顶角相等 | |
| B． | 角平分线上的点到这个角的两边的距离相等 | |
| C． | 如果a2=b2，那么a=b | |
| D． | 同旁内角互补，两直线平行 |
9．
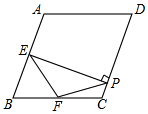如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC的度数为（ ）
如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC的度数为（ ）| A． | 50° | B． | 55° | C． | 60° | D． | 45° |
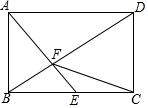如图，在矩形ABCD中，AB=$\sqrt{2}$，E是BC的中点，AE⊥BD于点F，则CF的长是$\sqrt{2}$．
某校计划组织师生共300人参加一次大型公益活动，如果租用6辆大客车和5辆小客车恰好全部坐满．已知每辆大客车的乘客座位数比小客车多17个．