Question

10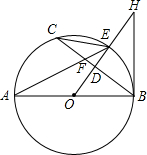．如图，AB为⊙O的直径，点D为弦BC的中点，OD的延长线交⊙O于点E，连接CE、AE、AE与BC交于点F，点H在OD的延长线上，且∠OHB=∠AEC．
（1）求证：BH与⊙O相切；
（2）若AE=4，tan∠A=$\frac{1}{2}$，求BF的长．

Answer 1

分析 （1）欲证明BH与⊙O相切，只要证明∠ABH=90°即可．
（2）连接EB，先求出EB、AB，由△EBF∽△EAB，得$\frac{BF}{AB}$=$\frac{BE}{AE}$，由此即可解决问题．

解答 （1）证明：∵D为BC中点，
∴OD⊥BC，
∴∠ODB=90°，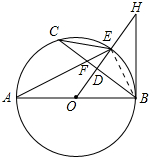
∴∠DOB+∠DBO=90°，
∵∠OHB=∠AEC，∠AEC=∠DBO，
∴∠OHB+∠DOB=90°，
∴∠OBH=90°，
∴OB⊥BH，
∴BH与⊙O相切．
（2）解：连接EB．∵AB是直径，
∴∠AEB=90°，
∵AE=4，tan∠A=$\frac{1}{2}$，
∴BE=2，AB=2$\sqrt{5}$，
∵OD⊥BC，
∴$\widehat{EB}$=$\widehat{EC}$，
∴∠EBF=∠EAB，
∵∠BEA=∠FEB，
∴△EBF∽△EAB，
∴$\frac{BF}{AB}$=$\frac{BE}{AE}$，即$\frac{BF}{2\sqrt{5}}$=$\frac{1}{2}$，
∴BF=$\sqrt{5}$．

点评 本题考查切线的性质、相似三角形的判定和性质、三角函数、勾股定理等知识，解题的关键是正确寻找相似三角形，利用相似三角形的性质解决问题，属于中考常考题型．