题目内容
8. 如图,点D、E分别在△ABC的边AB、AC上,且∠B=∠AED,若DE=3,AE=4,BC=9,则AB的长为12.
如图,点D、E分别在△ABC的边AB、AC上,且∠B=∠AED,若DE=3,AE=4,BC=9,则AB的长为12.
分析 根据已知∠ABC=∠AED,∠A=∠A,证明△ADE∽△ACB,根据相似三角形的性质,列出比例式,代入已知数据求出AB的长.
解答 解:∵∠ABC=∠AED,∠A=∠A,
∴ADE∽△ACB,
∴$\frac{AE}{AB}=\frac{DE}{BC}$,
∵DE=3,AE=4,BC=9,
∴AB=12,
故答案为:12.
点评 本题考查的是相似三角形的判定和性质,掌握由两个角对应相等的三角形相似是解题的关键,根据相似三角形的性质得到比例式是学生应重点掌握的.

练习册系列答案
相关题目
5.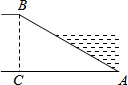 如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
 如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )
如图,河坝横断面迎水坡AB的坡比是1:$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是( )| A. | 9m | B. | 6m | C. | 6$\sqrt{3}$m | D. | 3$\sqrt{3}$m |
3.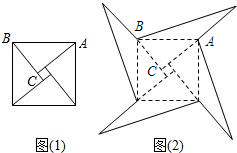 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 76 | B. | 72 | C. | 68 | D. | 52 |
20.下列说法正确的是( )
| A. | 1的平方根是1 | B. | 1是算术平方根是±1 | ||
| C. | -1的立方根是-1 | D. | (-1)2的平方根是-1 |
17.一个等腰三角形的两边分别为4cm和10cm,则该等腰三角形的周长为(单位:cm)( )
| A. | 14 | B. | 18 | C. | 24 | D. | 18或24 |
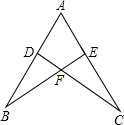 如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是:∠B=∠C.
如图,AB=AC,点D,E分别在AB,AC上,CD,BE交于点F,只添加一个条件使△ABE≌△ACD,添加的条件是:∠B=∠C.