题目内容
在直径是52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度CD为16cm,求油面宽度AB的长.

48cm.
【解析】
试题分析:因为圆柱形油槽装入油后形成弓形,可以考虑用垂径定理解答.
试题解析:由题意得出:OC⊥AB于点D,
由垂径定理知,点D为AB的中点,AB=2AD,
∵直径是52cm,
∴OB=26cm,
∴OD=OC﹣CD=26﹣16=10(cm),
由勾股定理知,
BD= =24(cm),
=24(cm),
∴AB=48cm.
考点:1.垂径定理的应用;2.勾股定理.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | … | 0 | 1 | 3 | 4 | … |
y | … | 2 | 4 | 2 | ﹣2 | … |
则下列判断中正确的是( )
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=﹣1时y>0
D.方程ax2+bx+c=0的负根在0与﹣1之间
 中,点
中,点 是
是 边的中点,且
边的中点,且 //
// ,则
,则 ___________.
___________. 
 轴交于
轴交于 、
、 两点,与
两点,与 轴交
轴交 点,点
点,点 ,点
,点 ,它的对称轴是直线
,它的对称轴是直线 .
.
 是线段
是线段 上的任意一点,当
上的任意一点,当 为等腰三角形时,求
为等腰三角形时,求 ,
, ,
, 作一圆弧,点
作一圆弧,点
 B.点
B.点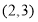 C.点
C.点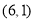 D.点
D.点
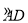 的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD
的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD

