题目内容
 如图,△ADC中,∠D=90°,B是AC边上一点,以AB为直径的⊙O与边CD,AD分别交于E、F两点,AE平分∠CAD.
如图,△ADC中,∠D=90°,B是AC边上一点,以AB为直径的⊙O与边CD,AD分别交于E、F两点,AE平分∠CAD.(1)求证:CD与⊙O相切;
(2)若ED=2,AD=4,求BE的长.
考点:切线的判定
专题:
分析:(1)连接OE,利用内错角相等证得线段OE∥AD,根据∠D=90°即可证得∠OED=∠D=90°,从而判定CD与⊙O相切;
(2)首先利用勾股定理求得AE的长,然后证得△AEB∽△ADE,利用相似三角形对应边的比相等求得线段BE的长.
(2)首先利用勾股定理求得AE的长,然后证得△AEB∽△ADE,利用相似三角形对应边的比相等求得线段BE的长.
解答: 解:(1)如图,连接OE,
解:(1)如图,连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠CAD,
∴∠OAE=∠EAD,
∴∠OEA=∠EAD,
∴OE∥AD,
∴∠OED=∠D=90°,
∴CD与⊙O相切;
(2)∵ED=2,AD=4,
∴AE=
=2
,
∵AB是⊙O的直径,
∴∠AEB=90°,
∵∠OAE=∠EAD,
∴△AEB∽△ADE,
∴
=
,
即:
=
,
解得:BE=
.
 解:(1)如图,连接OE,
解:(1)如图,连接OE,∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠CAD,
∴∠OAE=∠EAD,
∴∠OEA=∠EAD,
∴OE∥AD,
∴∠OED=∠D=90°,
∴CD与⊙O相切;
(2)∵ED=2,AD=4,
∴AE=
| ED2+AD2 |
| 5 |
∵AB是⊙O的直径,
∴∠AEB=90°,
∵∠OAE=∠EAD,
∴△AEB∽△ADE,
∴
| BE |
| ED |
| EA |
| AD |
即:
| BE |
| 2 |
2
| ||
| 4 |
解得:BE=
| 5 |
点评:本题考查了切线的判定,在解决切线问题时,常常连接圆心和切点,判定切线就是证明垂直,已知切线能得到垂直.

练习册系列答案
相关题目
已知点P(2,-3)关于y轴的对称点是P′(x,y),则点P′的坐标是( )
| A、(2,3) |
| B、(-2,3) |
| C、(-2,-3) |
| D、(2,-3) |
 如图,已知矩形纸片ABCD,AB=1.5,AD=1,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AD、AB交于点F、G(F≠D).
如图,已知矩形纸片ABCD,AB=1.5,AD=1,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AD、AB交于点F、G(F≠D).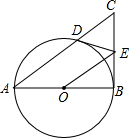 如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边上的动点,连接DE,OE.
如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边上的动点,连接DE,OE. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,求AD的长.
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,求AD的长. 如图,点A′、B′、C′、D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′,求证:A′C′与B′D′互相垂直且相等.
如图,点A′、B′、C′、D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′,求证:A′C′与B′D′互相垂直且相等. 超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想用自己所学的知识检测车速,如图,他们将观测点设在到公路l的距离为0.1千米的P处,这时,一辆轿车由西向东匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°.如果这段高速公路的限速是每小时90千米(即最高时速不超过90千米),试判断此车是否超速?
超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想用自己所学的知识检测车速,如图,他们将观测点设在到公路l的距离为0.1千米的P处,这时,一辆轿车由西向东匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°.如果这段高速公路的限速是每小时90千米(即最高时速不超过90千米),试判断此车是否超速?