题目内容
1.已知:关于x,y的二元一次方程ax+by=3(ab≠0)的一个解为$\left\{\begin{array}{l}x=1\\ y=-1\end{array}\right.$,求$\frac{a-b}{a}÷(a-\frac{{2ab-{b^2}}}{a})$的值.分析 先把x=1,y=-1代入方程ax+by=3得出a-b=3,再把原式进行化简,把a-b=3代入进行计算即可.
解答 解:∵关于x,y的二元一次方程ax+by=3(ab≠0)的一个解为$\left\{\begin{array}{l}x=1\\ y=-1\end{array}\right.$,
∴a-b=3.
原式=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$,
当a-b=3时,原式=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
12.本溪电视台某日发布的当天的天气预报,我市Ⅱ各地区当天最高气温(℃)统计如表:
那么这些城市当天的最高气温的众数和中位数分别是13℃,13℃.
| 气温(℃) | 10 | 11 | 12 | 13 | 14 | 15 | 17 |
| 频数 | 1 | 1 | 1 | 3 | 2 | 2 | 1 |
16.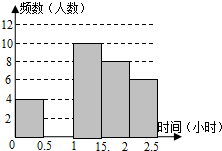 我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
(1)在表格中,a=12,b=0.2;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
 我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
我县某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.| 时间(小时) | 频数(人数) | 频率 |
| 0≤t<0.5 | 4 | 0.1 |
| 0.5≤t<1 | a | 0.3 |
| 1≤t<1.5 | 10 | 0.25 |
| 1.5≤t<2 | 8 | b |
| 2≤t<2.5 | 6 | 0.15 |
| 合计 | 1 |
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,约有多少学生在1.5小时以内完成了家庭作业.
6.雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”.已知1微米等于1米的一百万分之一,那么2.5微米用科学记数法可表示为( )
| A. | 0.25×10-7米 | B. | 2.5×10-6米 | C. | 25×10-5米 | D. | 2.5×10-5米 |
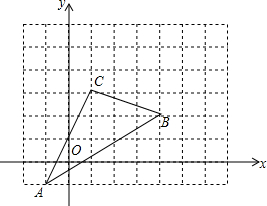 如图,三角形ABC在直角坐标系中,
如图,三角形ABC在直角坐标系中,