题目内容
4. 如图,在四边形ABCD是边长为4的正方形,点E在边BC上(不与点B,点C重合),∠AEF=90°,且EF交正方形外角的平分线于点F,AF与CD相交于点H.下列结论:①∠BAE=∠FEC;②AE=EF;③△CEF的面积最大值为2;④BE+DH=EH.其中正确结论的个数是( )
如图,在四边形ABCD是边长为4的正方形,点E在边BC上(不与点B,点C重合),∠AEF=90°,且EF交正方形外角的平分线于点F,AF与CD相交于点H.下列结论:①∠BAE=∠FEC;②AE=EF;③△CEF的面积最大值为2;④BE+DH=EH.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 在BA上截取BM=BE,如图1,易得△BEF为等腰直角三角形,则∠BME=45°,所以∠AME=135°,再利用等角的余角相等得到∠BAE=∠FEC,则可对①进行判断;于是根据“ASA”可判断△AME≌△ECF,则根据全等三角形的性质可对②进行判断;设BE=x,则BM=x,AM=AB-BM=4-x,利用三角形面积公式得到S△AME=$\frac{1}{2}$•x•(4-x),则根据二次函数的性质可判断当x=2时,S△AME有最大值2,则利用△AME≌△ECF可对③进行判断;判断△AEF为等腰直角三角形得到∠EAF=45°,延长EB到G点,使BG=DH,如图2,易得△ABG≌△ADH,则AG=AH,∠BAG=∠DAH,于是根据“SAS”证明△AEG≌△AEH,所以EG=EH,于是得到BE+DH=EH,则可对④进行判断.
解答 解:在BA上截取BM=BE,如图1,
∵四边形ABCD为正方形,
∴∠B=90°,BA=BC,
∴△BEF为等腰直角三角形,
∴∠BME=45°,
∴∠AME=135°,
∵BA-BM=BC-BE,
∴AM=CE,
∵CF为正方形外角平分线,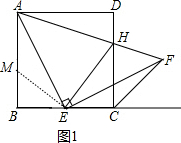
∴∠DCF=45°,
∴∠ECF=135°,
∵AE⊥EF,
∴∠AEB+∠FEC=90°,
而∠AEB+∠BAE=90°,
∴∠BAE=∠FEC,所以①正确;
在△AME和△ECF中
$\left\{\begin{array}{l}{∠MAE=∠CEF}\\{AM=EC}\\{∠AME=∠ECF}\end{array}\right.$,
∴△AME≌△ECF,
∴AE=EF,所以②正确;
设BE=x,则BM=x,AM=AB-BM=4-x,
S△AME=$\frac{1}{2}$•x•(4-x)=-$\frac{1}{2}$(x-2)2+2,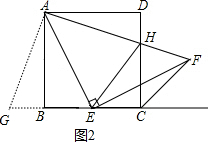
当x=2时,S△AME有最大值2,
而△AME≌△ECF,
∴S△AME=S△CEF,
∴S△CEF有最大值2,所以③正确;
∵AE=EF,AE⊥EF,
∴△AEF为等腰直角三角形,
∴∠EAF=45°,
延长EB到G点,使BG=DH,如图2,
在△ABG和△ADH中
$\left\{\begin{array}{l}{AB=AD}\\{∠ABG=∠ADH}\\{BG=DH}\end{array}\right.$,
∴△ABG≌△ADH,
∴AG=AH,∠BAG=∠DAH,
而∠DAH+∠BAH=90°,
∴∠BAG+∠BAH=90°,即∠GAH=90°,
∴∠GAE=90°-∠EAF=45°,
∴∠GAE=∠HAE,
在△AEG和△AEH中
$\left\{\begin{array}{l}{AG=AH}\\{∠EAG=∠EAH}\\{AE=AE}\end{array}\right.$,
∴△AEG≌△AEH,
∴EG=EH,即BE+BG=EH,
∴BE+DH=EH,所以④正确.
故选D.
点评 本题考查了四边形的综合题:熟练掌握正方形的性质和二次函数的性质;能灵活运用全等三角形的知识解决线段线段的问题.构建△AME与△EFC全等是判断①②③的关键;而构建△AEG与△AEH全等是判断④的关键.

 如图.点A的坐标是( )
如图.点A的坐标是( )| A. | (2,3) | B. | (-2,-3) | C. | (3,2) | D. | (-3,-2) |
| A. | 3a | B. | a | C. | 4a | D. | 都不对 |
| 项目 | 着装 | 队形 | 精神风貌 |
| 成绩(分) | 90 | 94 | 92 |
 点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点.
点P是等腰直角三角形ABC底边BC上一点,过点P作BA、AC的垂线,垂足为E、F,设D为BC的中点. 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.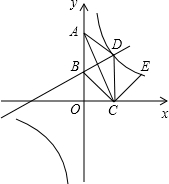 如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.
如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.