题目内容
5.请仔细观察图中有关辅助线的画法,从中任选一个,证明多边形内角和定理:n边形的内角和等于(n-2)•180,下面已给出已知、求证,请把你选择的方法及证明多边形内角和定理的过程写出来.方法一:在n边形A1 A2 A3 A4 A5…An中任取一点O,连接O与各个顶点.
方法二:作过顶点A的所有对角线.
方法三:在n边形的边A1A2上任取一点P,连接这点与各个顶点.
已知:n边形A1 A2 A3 A4 A5…An,求证:n边形A1 A2 A3 A4 A5…An的内角和等于(n-2)•180°.
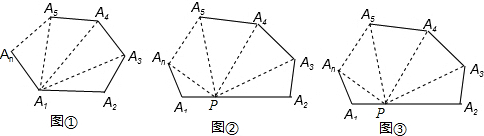
分析 根据图形割补法,可得三角形,根据三角形的内角和,可得答案.
解答 证明:如图: ,
,
∵(n-3)条对角线把n边形分成(n-2)个三角形,
∴∠A1+∠A2+∠A3++…+∠An=(n-2)•180°.
点评 本题考查了多边形内角与外角,利用分割法把多边形转化成三角形是解题关键.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
16.已知△ABC≌△DEF,且∠A=60°,∠E=50°,则∠F等于( )
| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
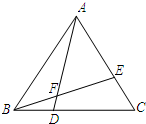 如图,△ABC为等边三角形,D、E是BC、AC边上的点,且BD=CE,线段AD、BE交于F,
如图,△ABC为等边三角形,D、E是BC、AC边上的点,且BD=CE,线段AD、BE交于F,