题目内容
3.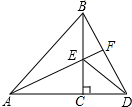 如图,在△ABD中,BC⊥AD于点C,E为BC上一点,AE=BD,EC=CD,延长AE交BD于点F.求证:AF⊥BD.
如图,在△ABD中,BC⊥AD于点C,E为BC上一点,AE=BD,EC=CD,延长AE交BD于点F.求证:AF⊥BD.
分析 只要证明△ACE≌△BCD(HL),即可推出∠CAE=∠CBD,由∠CAE+∠AEC=90°,∠AEC=∠BEF,推出∠CBD+∠BEF=90°,推出∠EFB=90°即可.
解答 证明: ∵BC⊥AD,
∵BC⊥AD,
∴∠ACE=∠BCD=90°,
在Rt△ACE和Rt△BCD中,
$\left\{\begin{array}{l}{AE=BD}\\{EC=CD}\end{array}\right.$,
∴△ACE≌△BCD(HL),
∴∠CAE=∠CBD,
∵∠CAE+∠AEC=90°,∠AEC=∠BEF,
∴∠CBD+∠BEF=90°,
∴∠EFB=90°,
∴AF⊥BD.
点评 本题考查全等三角形的判定和性质、直角三角形的判定等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.为了解南阳市某小区小孩暑期的学习情况,王老师随机调查了该小区8个小孩某天的学习时间,结果如下(单位:小时):1.5,1.5,2,2.5,3,4,4.5,5,关于这组数据,下列结论错误的是( )
| A. | 众数是1.5 | B. | 中位数是3 | C. | 平均数是3 | D. | 方差是$\frac{13}{8}$ |
12.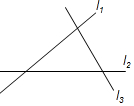 如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
 如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )| A. | 1处 | B. | 2处 | C. | 3处 | D. | 4处 |
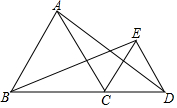 如图,点C在BD边上,且△ABC和△ECD都是等边三角形,图中有一对全等三角形可以看成是旋转变换得到的.一对全等三角形是△BCE≌△ACD,其旋转中心是点C,旋转角的度数是60°.
如图,点C在BD边上,且△ABC和△ECD都是等边三角形,图中有一对全等三角形可以看成是旋转变换得到的.一对全等三角形是△BCE≌△ACD,其旋转中心是点C,旋转角的度数是60°.



 已知在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,AC=BC.如图,当A(0,-2),C(1,0),点B在第四象限时,则点B的坐标为(3,-1).
已知在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,AC=BC.如图,当A(0,-2),C(1,0),点B在第四象限时,则点B的坐标为(3,-1).