题目内容
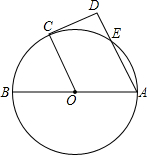 如图,已知AB是⊙O的直径,E是⊙O上一点,C是
如图,已知AB是⊙O的直径,E是⊙O上一点,C是 |
| BE |
(1)试判断OC与AD的关系,并说明理由.
(2)试判断CD与⊙O的关系,并说明理由.
考点:切线的判定
专题:
分析:(1)运用圆周角定理证明∠BOC=∠BAD,问题即可解决.
(2)运用平行线的性质证明OC⊥CD,问题即可解决.
(2)运用平行线的性质证明OC⊥CD,问题即可解决.
解答: 解:(1)如图,连接OE;
解:(1)如图,连接OE;
∵C是
的中点,
∴∠BOC=∠EOC,∠BOE=2∠BOC;
又∵∠BAE=
∠BOE=∠BOC,
即∠BAE=∠BOC,
∴OC∥AD.
(2)∵OC∥AD,且CD⊥AE于D,
∴OC⊥CD,
∴CD为⊙O的切线.
 解:(1)如图,连接OE;
解:(1)如图,连接OE;∵C是
 |
| BE |
∴∠BOC=∠EOC,∠BOE=2∠BOC;
又∵∠BAE=
| 1 |
| 2 |
即∠BAE=∠BOC,
∴OC∥AD.
(2)∵OC∥AD,且CD⊥AE于D,
∴OC⊥CD,
∴CD为⊙O的切线.
点评:该题主要考查了切线的判定、圆周角定理及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
下列四个点中,在正比例函数y=-
x的图象上的点是( )
| 2 |
| 3 |
| A、(3,2) |
| B、(2,2) |
| C、(-3,2) |
| D、(1,-2) |
在下列各数中:0,
,-π,
,0.3215…中,无理数的个数是( )
| 8 |
| 11 |
| 3 |
| A、2个 | B、3个 | C、4个 | D、5个 |
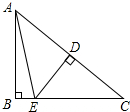 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,则∠C的度数为( )
如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,则∠C的度数为( )| A、45° | B、37° |
| C、60° | D、30° |