题目内容
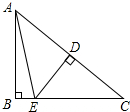 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,则∠C的度数为( )
如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=16°,则∠C的度数为( )| A、45° | B、37° |
| C、60° | D、30° |
考点:线段垂直平分线的性质
专题:
分析:根据线段垂直平分线性质得出AE=CE,推出∠C=∠CAE,根据三角形内角和定理求出即可.
解答:解:∵ED是AC的垂直平分线,
∴AE=CE,
∴∠C=∠EAC,
∵∠B=90°,∠BAE=16°,
∴2∠C=90°-16°=74°,
∴∠C=37°,
故选B.
∴AE=CE,
∴∠C=∠EAC,
∵∠B=90°,∠BAE=16°,
∴2∠C=90°-16°=74°,
∴∠C=37°,
故选B.
点评:本题考查了线段垂直平分线性质,三角形内角和定理,等腰三角形的性质的应用,解此题的关键是推出∠C=∠CAE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算正确的是( )
| A、a2+a3=a5 |
| B、a6÷a3=a2 |
| C、(a+b)2=a2+b2 |
| D、(-2a3)2=4a6 |
 已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么2的对面数字是
已知一不透明的正方体的六个面上分别写着1至6六个数字,如图是我们能看到的三种情况,那么2的对面数字是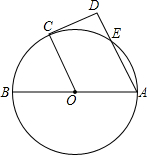 如图,已知AB是⊙O的直径,E是⊙O上一点,C是
如图,已知AB是⊙O的直径,E是⊙O上一点,C是