题目内容
在平面直角坐标系中,O为原点,若一次函数y=kx+b的图象交x轴于点A(-2,0),交y轴于点B,△AOB面积为8,则该函数解析式为 .
考点:待定系数法求一次函数解析式
专题:计算题
分析:设B点坐标为(0,t),根据三角形面积公式得到
•2•|t|=8,解得t=8或-8,则B点坐标为(0,8)或(0,-8),然后利用待定系数法求经过A(-2,0),B(0,8)或经过A(-2,0),B(0,-8)的直线解析式.
| 1 |
| 2 |
解答:解:设B点坐标为(0,t),
∵△AOB面积为8,
∴
•2•|t|=8,解得t=8或-8,
∴B点坐标为(0,8)或(0,-8),
设一次函数解析式为y=kx+b,
当直线y=kx+b经过A(-2,0),B(0,8)时,则
,解得
,所以一次函数解析式为y=4x+8;
当直线y=kx+b经过A(-2,0),B(0,-8)时,则
,解得
,所以一次函数解析式为y=-4x-8,
综上所述,该函数解析式为y=4x+8或y=-4x-8.
故答案为y=4x+8或y=-4x-8.
∵△AOB面积为8,
∴
| 1 |
| 2 |
∴B点坐标为(0,8)或(0,-8),
设一次函数解析式为y=kx+b,
当直线y=kx+b经过A(-2,0),B(0,8)时,则
|
|
当直线y=kx+b经过A(-2,0),B(0,-8)时,则
|
|
综上所述,该函数解析式为y=4x+8或y=-4x-8.
故答案为y=4x+8或y=-4x-8.
点评:本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,虚线部分是小刚作的辅助线,你认为线段CD( )
如图,虚线部分是小刚作的辅助线,你认为线段CD( )| A、是AC边上的高 |
| B、是BC边上的高 |
| C、是AB边上的高 |
| D、不是△ABC的高 |
二次函数y=2x2-4x+m的图象上有点A(2013,a),B (2014,b),关于a,b的大小关系,下列正确的是( )
| A、a>b |
| B、a<b |
| C、a=b |
| D、m的取值不确定,无法确定a,b的大小 |
圆内接四边形ABCD的四个内角之比可能是( )
| A、1:2:3:4 |
| B、1:3:4:5 |
| C、2:3:4:5 |
| D、2:3:5:4 |
下列说法中正确的是( )
| A、1是最小的有理数 |
| B、0既不是正数也不是负数 |
| C、整数只包括正整数和负整数 |
| D、-1是最大的负有理数 |
已知二次函数y=a(x-1)2-b(a≠0)有最小值
,则a、b的大小比较为( )
| 1 |
| 2 |
| A、a>b | B、a<b |
| C、a=b | D、不能确定 |
若一次函数y=kx+3的图象过点P(2,-1),则k的值( )
| A、2 | B、-2 | C、3 | D、-3 |
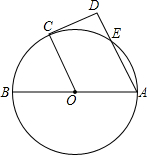 如图,已知AB是⊙O的直径,E是⊙O上一点,C是
如图,已知AB是⊙O的直径,E是⊙O上一点,C是