题目内容
【题目】春天来了,我校计划组织师生共![]() 人坐
人坐![]() 、
、![]() 两种型号的大巴车外出春游,且
两种型号的大巴车外出春游,且![]() 型车每辆租金为
型车每辆租金为![]() 元,
元,![]() 型车每辆租金为
型车每辆租金为![]() 元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租
元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人,若租
人,若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人.
人.
(1)请问![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车各有几座?
型大巴车各有几座?
(2)现学校决定租两种型号的大巴车共![]() 辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过
辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过![]() 元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了
元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了![]() 型大巴车
型大巴车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
【答案】(1)每辆![]() 型客车有
型客车有![]() 个座位,每辆
个座位,每辆![]() 型客车有
型客车有![]() 个座位;(2)共有
个座位;(2)共有![]() 种租车方案,租
种租车方案,租![]() 型客车
型客车![]() 辆,
辆,![]() 型客车
型客车![]() 辆最省钱,最低费用为
辆最省钱,最低费用为![]() 元.
元.
【解析】
(1)设1辆A型大巴车有x个座,1辆B型大巴车有y个座,根据“租2辆A型与3辆B型大巴车恰好能坐下195人,若租3辆A型与2辆B型大巴车恰好能坐下180人”即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)先根据总价=单价×数量求出w与x的关系式,再由至少可有1600个座位及总经费不能超过![]() 元列出相应的不等式组从而求出x的取值范围,得到x的整数解,最后由函数的增减性确定出最省钱的方案即可.
元列出相应的不等式组从而求出x的取值范围,得到x的整数解,最后由函数的增减性确定出最省钱的方案即可.
(1)设每辆![]() 型客车有
型客车有![]() 个座位,每辆
个座位,每辆![]() 型客车有
型客车有![]() 个座位,
个座位,
由题意,得:![]()
解得:![]()
答:每辆![]() 型客车有
型客车有![]() 个座位,每辆
个座位,每辆![]() 型客车有
型客车有![]() 个座位.
个座位.
(2)根据题意,得
![]()
解得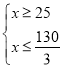
![]() (
(![]() 为正整数)
为正整数)
![]()
![]()
![]() 随
随![]() 的增大而增大
的增大而增大
![]() 当
当![]() 时,
时,![]() 有最小值,最小值为
有最小值,最小值为![]()
答:共有![]() 种租车方案,租
种租车方案,租![]() 型客车
型客车![]() 辆,
辆,![]() 型客车
型客车![]() 辆最省钱,最低费用为
辆最省钱,最低费用为![]() 元.
元.

【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息解答下列问题:
组别 | 阅读时间 | 频数(人数) |
|
| 8 |
|
| 20 |
|
| 24 |
|
|
|
|
|
|
|
| 4 |
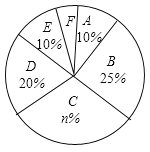
(1)图表中的![]() ______,
______,![]() ______;
______;
(2)扇形统计图中![]() 组所对应的圆心角为______度;
组所对应的圆心角为______度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?