题目内容
某校要从九年级一班和二班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
一班:168 167 170 165 168 166 171 168 167 170
二班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表:
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
一班:168 167 170 165 168 166 171 168 167 170
二班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表:
| 班级 | 平均数 | 方差 | 中位数 | 极差 |
| 一班 | 168 | 168 | 6 | |
| 二班 | 168 | 3.8 |
考点:方差,算术平均数,中位数,极差
专题:计算题
分析:(1)利用方差公式即可求出一班样本的方差;将二班样本中的十个数据先按从小到大的顺序排列,求出中间两个数的平均数就是二班样本的中位数;将二班样本中最大的数据减去最小的数据就是极差.
(2)可以从方差角度进行分析,从而确定哪一个班能被选取.
(2)可以从方差角度进行分析,从而确定哪一个班能被选取.
解答:解:(1)①由方差公式S2=
[(x1-
)2+[(x2-
)2+[(x3-
)2+…+[(xn-
)2]
得:S12=
[(168-168)2+(167-168)2+(170-168)2+(165-168)2+(168-168)2
+(166-168)2+(171-168)2+(168-168)2+(167-168)2+(170-168)2]
=
(0+1+4+9+0+4+9+0+1+4)
=3.2.
②将165 167 169 170 165 168 170 171 168 167按从小到大的顺序排列,
得:165 165 167 167 168 168 169 170 170 171.
最中间的两个数为168和168,
=168.这组数据的中位数是168.
③数据165 167 169 170 165 168 170 171 168 167中的最大值为171,最小值为165.
∴极差=171-165=6.
故答案为3.2、168、6.
(2)因为一班与二班的样本平均数、中位数、极差均相同,
且一班样本的方差3.2小于二班样本的方差3.8,
所以一班的同学身高相对比较整齐,故一班能被选取.
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
得:S12=
| 1 |
| 10 |
+(166-168)2+(171-168)2+(168-168)2+(167-168)2+(170-168)2]
=
| 1 |
| 10 |
=3.2.
②将165 167 169 170 165 168 170 171 168 167按从小到大的顺序排列,
得:165 165 167 167 168 168 169 170 170 171.
最中间的两个数为168和168,
| 168+168 |
| 2 |
③数据165 167 169 170 165 168 170 171 168 167中的最大值为171,最小值为165.
∴极差=171-165=6.
故答案为3.2、168、6.
(2)因为一班与二班的样本平均数、中位数、极差均相同,
且一班样本的方差3.2小于二班样本的方差3.8,
所以一班的同学身高相对比较整齐,故一班能被选取.
点评:本题考查了如何求方差、中位数、极差,以及如何运用这些知识解决问题,属于基本题,而求中位数往往容易忘记先排序,需注意.

练习册系列答案
相关题目
2014年1月30日晚,全国约有7.04亿人观看中央电视台播出的马年春节联欢晚会,7.04亿用科学记数法可表示为( )
| A、7.04×107 |
| B、7.04×108 |
| C、7.04×109 |
| D、7.04×1010 |
 如图,在△ABC中,BD⊥AC,AB=6,AC=5
如图,在△ABC中,BD⊥AC,AB=6,AC=5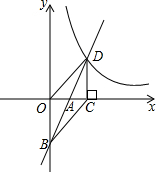 如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y=
如图,在平面直角坐标系中,一次函数y=2x+b(b<0)的图象与坐标轴交于A、B两点,与函数y= 如图,是八年级(3)班学生参加课外活动人数的扇形统计图,如果参加艺术类的人数是16人,那么参加其它活动的人数是
如图,是八年级(3)班学生参加课外活动人数的扇形统计图,如果参加艺术类的人数是16人,那么参加其它活动的人数是