Question

【题目】在平面直角坐标系中，直线与轴相交于点，与轴相交于点，以点为圆心，线段的长为半径画弧，与直线位于第一象限的部分相交于点，则点的坐标为_______．

Answer 1

【答案】

【解析】

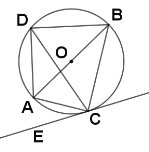
先求出OA、OB的长度，连接AB，过点C作CD⊥y轴于D，设D（0，m），得到CD=m+1，BD=m-2，BC=OA=，利用勾股定理建立等式求出m即可得到点C的坐标.

令中y=0得x=，令x=0得y=2，

∴A(，0)，B(0,2)，

∴OA=，OB=2，

连接AB，过点C作CD⊥y轴于D，

设D（0，m），

∵点C在，

∴CD=CE=m+1，

∵BD=m-2，BC=OA=， ,

∴，

解得m=或m=（负值舍去），

∴CD=m+1=，

∴点C的坐标是（，），

故答案为：（，）.