题目内容
【题目】已知m,n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a,n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ac=a,b+c≥2a,n≤﹣![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)b=1,c=1;(2)![]() ;(3)-
;(3)-![]() ≤a≤-
≤a≤-![]() .
.
【解析】
(1)由已知求出n,根据方程根的定义将m,n,a的值代入方程即可求解;
(2)根据方程根的定义将m,n的值代入方程消去c求解得到![]() ,再利用m+n=1,消去m,即可求出b只用字母a、n表示代数式,
,再利用m+n=1,消去m,即可求出b只用字母a、n表示代数式,
(3)将(2)结论![]() 代入方程
代入方程![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,继而可得
,继而可得![]() ,根据n的取值范围即可确定a的取值范围.
,根据n的取值范围即可确定a的取值范围.
(1)因为m,n分别是关于x的一元二次方程![]() 与
与![]() 的一个根,
的一个根,
所以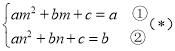 ,
,
由m=n+1,m=2得n = 1
把n=1,m=2,a = -1,代入(*)得,
![]() ,
,
解得![]() ;
;
(2)由(1)的方程组(*)中①-②,得
![]() ,
,
![]() ,由m=n+1,得m-n=1,
,由m=n+1,得m-n=1,
故a![]() ,
,
所以![]() ,
,
从而![]() ;
;
(3)把![]() 代入方程组(*)中②,得
代入方程组(*)中②,得
![]() ,
,
由![]() ≥2a得
≥2a得
![]() ≥2a,
≥2a,
当a<0时,n≥-1,
由n≤-![]() 得,-1≤n≤-
得,-1≤n≤-![]() ,
,
由![]() ,且
,且![]() ,得
,得
![]() ,
,
整理得,![]() ,因为a<0
,因为a<0
所以,![]() ,
,
即![]() ,
,
由于![]() 在-1≤n≤-
在-1≤n≤-![]() 时随n的增大而增大,
时随n的增大而增大,
所以当n= -1时,a= -![]() ,当n= -
,当n= -![]() 时,a= -
时,a= -![]()
即-![]() ≤a≤-
≤a≤-![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目