题目内容
10.直线y=ax+b经过第二、三、四象限,则下列结论正确的是( )| A. | $\sqrt{(a+b)^{2}}$=a+b | |
| B. | 点(a,b)在第一象限 | |
| C. | 抛物线y=ax2+bx+c的对称轴经过第二、三象限 | |
| D. | 反比例函数y=$\frac{a}{x}$,当x>0时,函数值随x的增大而减小 |
分析 先根据直线y=ax+b经过第二、三、四象限可知a<0,b<0,再对各选项进行逐一分析即可.
解答 解:∵直线y=ax+b经过第二、三、四象限,
∴a<0,b<0.
A、∵a<0,b<0,∴$\sqrt{{(a+b)}^{2}}$=-(a+b),故本选项错误;
B、∵a<0,b<0,∴点(a,b)在第三象限,故本选项错误;
C、∵a<0,b<0,∴抛物线y=ax2+bx+c的对称轴x=-$\frac{b}{2a}$<0,∴对称轴经过第二、三象限,故本选项正确;
D、∵a的符号不确定,故此函数的增减性无法判断,故本选项错误.
故选C.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k<0,b<0时函数的图象经过第二、三、四象限是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.在$\frac{1}{4}$,-1,0,2这四个数中,属于负数的是( )
| A. | $\frac{1}{4}$ | B. | -1 | C. | 0 | D. | 2 |
5.下列图形,既是轴对称图形,又是中心对称图形的是( )
| A. | 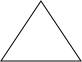 | B. | 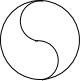 | C. |  | D. | 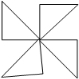 |
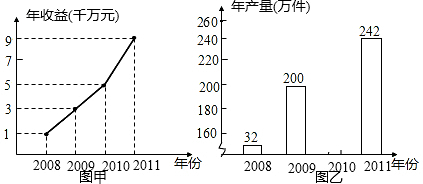
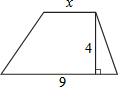 如图所示,梯形上底的长是x,下底的长是9,高是4,梯形面积y与底长x之间的关系式是y=2x+18.
如图所示,梯形上底的长是x,下底的长是9,高是4,梯形面积y与底长x之间的关系式是y=2x+18.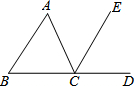 写出图中∠B的一个同位角∠ECD或∠ACD.
写出图中∠B的一个同位角∠ECD或∠ACD.