��Ŀ����
ij���µ꽫����Ϊ30Ԫ��һ�ֳ�����40Ԫ�۳���ƽ��ÿ�����۳�600����������������ֳ����ۼ�ÿ����1Ԫ����������������10��.
��1��д������������y����λ��Ԫ�����ۼ�x����λ��Ԫ/����֮��ĺ�������ʽ.
��2�������ۼ۶�Ϊ45Ԫʱ������������������������.
��3�����µ�������������������300��������£�ʹ����������ﵽ10000Ԫ�����ۼ�Ӧ��Ϊ���٣�
��4�������ۼ۶�Ϊ����Ԫʱ���������������������.
��1��y=-10x2+1300x-30000����2��550���� 8250Ԫ����3��50Ԫ����4��65Ԫ��12250Ԫ.
��������
�����������1��������ÿ�������ۼ�ΪxԪ��������������ۼ�ÿ����1Ԫ�����������ͼ���10�����г�������ϵʽ��
��2�����ۼ�Ϊ45Ԫ����������5Ԫ�����뼴��������������������
��3����y=10000���ⷽ�̼��ɣ�
��4�����䷽��������κ��������ֵ���ɣ�
�����������1��y=(x-30)(600-10�� )=-10x2+1300x-30000;
)=-10x2+1300x-30000;
���ۼ�Ϊ45Ԫ����������5Ԫ������������=600-10��5=550��������
��������:y=-10��452+1300��45-30000=8250��Ԫ����
��3����y=-10x2+1300x-30000 ����y=10000����-10x2+1300x-30000=10000 ��
��x2-130x+4000=0����(x-50)(x-80)=0����x=50��x=80��
���ۼ�x=50ʱ��������=600��10��(50-40)=500��
���ۼ�x=80ʱ��������=600��10��(80-40)=200<300���������⣬Ӧ��ȥ��
��4����y=-10x2+1300x-30000=-10(x-65)2+12250��
�൱x=65ʱ��y �����ֵ12250��
����ÿ�������ۼ�Ϊ65Ԫʱ�����������Ϊ12250Ԫ��
���㣺���κ�����Ӧ�ã�

��ͼ����ƽ���ı���ABCD�У��� E�DZ�AD���е㣬EC���Խ���BD�ڵ�F����EF�UCF���ڣ� ��

A��3��2 B��3��1 C��1��1 D��1��2
�������б���Ķ�Ӧֵ���жϷ���ax2+bx+c=0��a��0��a��b��cΪ������һ����ķ�Χ�ǣ� ��
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ��0.06 | ��0.02 | 0.03 | 0.09 |
A��3��x��3.23 B�� 3.23��x��3.24 C�� 3.24��x��3.25 D�� 3.25��x��3.26
 ��
�� ��ͼ����
��ͼ���� ��Ľ�������Ϊ ��
��Ľ�������Ϊ �� ���ף�������ʱ��
���ף�������ʱ�� ���룩�ĺ�������ʽΪ
���룩�ĺ�������ʽΪ ����ôС����ߵ�ʱ�������ĸ߶��ǣ� ��
����ôС����ߵ�ʱ�������ĸ߶��ǣ� �� ��y��Ľ��㣬��B����������������һ��.��AB//x�ᣬ����ABΪ�ߵĵȱ�������ABC���ܳ�Ϊ .
��y��Ľ��㣬��B����������������һ��.��AB//x�ᣬ����ABΪ�ߵĵȱ�������ABC���ܳ�Ϊ .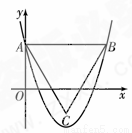

 B��
B�� C��
C�� D��
D��
 ��
�� ��2��
��2��