题目内容
1.在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,应选择的关系式是( )| A. | c=$\frac{a}{sinA}$ | B. | c=$\frac{a}{cosA}$ | C. | c=a•tanA | D. | c=$\frac{a}{tanA}$ |
分析 作出图形,然后根据锐角的正弦等于对边比斜边解答.
解答 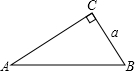 解:如图,∵已知∠A和a,求c,
解:如图,∵已知∠A和a,求c,
∴sinA=$\frac{a}{c}$,
∴c=$\frac{a}{sinA}$.
故选A.
点评 本题考查了锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,作出图形更形象直观.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
13.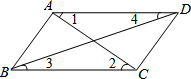 如图所示,下列四组条件中,不能判定AD∥BC的是( )
如图所示,下列四组条件中,不能判定AD∥BC的是( )
 如图所示,下列四组条件中,不能判定AD∥BC的是( )
如图所示,下列四组条件中,不能判定AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠ABC=∠ADC | D. | ∠BAD+∠ABC=180° |
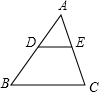 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=9,$\frac{AD}{BD}$=$\frac{3}{4}$,则EC的长是
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=9,$\frac{AD}{BD}$=$\frac{3}{4}$,则EC的长是