题目内容
11.若3m=2,3n=5,则32m-n=$\frac{4}{5}$.分析 首先根据幂的乘方的运算法则,求出32m、3-n的值各是多少;然后根据同底数幂的乘法法则计算即可.
解答 解:∵3m=2,3n=5,
∴32m=22=4,3-n=${5}^{-1}=\frac{1}{5}$,
∴32m-n=4×$\frac{1}{5}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 (1)此题主要考查了同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,要熟练掌握,解答此题的关键是要明确:(1)底数必须相同;(2)按照运算性质,只有相乘时才是底数不变,指数相加.
(2)此题还考查了同底数幂的除法法则:同底数幂相除,底数不变,指数相减,要熟练掌握,解答此题的关键是要明确:①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.
(3)此题还考查了幂的乘方和积的乘方,要熟练掌握,解答此题的关键是要明确:①(am)n=amn(m,n是正整数);②(ab)n=anbn(n是正整数).

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
1.在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,应选择的关系式是( )
| A. | c=$\frac{a}{sinA}$ | B. | c=$\frac{a}{cosA}$ | C. | c=a•tanA | D. | c=$\frac{a}{tanA}$ |
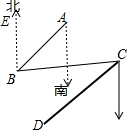 如图,B处在A处南偏西45°的方向,C处在B处的北偏东80°,若D处在C处的南偏西45°的方向,试说明:CD∥AB.
如图,B处在A处南偏西45°的方向,C处在B处的北偏东80°,若D处在C处的南偏西45°的方向,试说明:CD∥AB.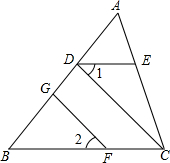 如图,已知:∠ADE=∠B,∠2=∠1,GF⊥AB,则CD⊥AB吗?请说明理由.
如图,已知:∠ADE=∠B,∠2=∠1,GF⊥AB,则CD⊥AB吗?请说明理由.