题目内容
11.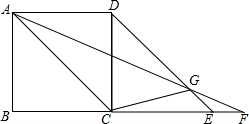 如图,正方形ABCD的边BC的延长线满足CE=DC,CF=AC,连结AF、DE交于点G,连结CG.试证明△DCG是等腰三角形.
如图,正方形ABCD的边BC的延长线满足CE=DC,CF=AC,连结AF、DE交于点G,连结CG.试证明△DCG是等腰三角形.
分析 由正方形的性质得出∠BCD=∠BAD=∠ADC=90°,DC=AD,得出AC=$\sqrt{2}$CD,证出△DCE是等腰直角三角形,得出∠CDE=∠CED=45°,DE=$\sqrt{2}$CD=$\sqrt{2}$CE,得出AC=DE,证出CF=DE,再证出EF=EG,即可得出结论.
解答 证明:∵四边形ABCD是正方形,
∴∠BCD=∠BAD=∠ADC=90°,DC=AD,
∴AC=$\sqrt{2}$CD,∠DCE=90°,
∴∠ACE=45°+90°=135°,
∵CF=AC,
∴∠F=∠CAF=$\frac{1}{2}$(180°-135°)=22.5°,
∴∠DAG=45°-22.5°=22.5°,
∵CE=DC,
∴△DCE是等腰直角三角形,
∴∠CDE=∠CED=45°,DE=$\sqrt{2}$CD=$\sqrt{2}$CE,
∴AC=DE,
∵CF=AC,
∴CF=DE,
∵∠CEG=∠F+∠EGF,
∴∠EGF=45°-22.5°=22.5°=∠F,
∴EF=EG,
∴CF-EF=DE-GE,
∴CE=DG,
∴CD=DG,
即△DCG是等腰三角形.
点评 本题考查了正方形的性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2.根据下列条件,得不到平行四边形的是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,AB=CD | C. | AB=CD,AD∥BC | D. | AB∥CD,AD∥BC |
19. 如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
 如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )
如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( )| A. | 35° | B. | 55° | C. | 70° | D. | 105° |
3.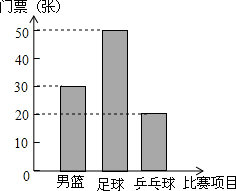 下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:
下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:
(1)其中观看足球比赛的门票有50张,观看乒乓球比赛的门票占全部门票的20%;
(2)公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地完全相同且充分洗匀),问员工小华抽到男篮门票的概率是$\frac{3}{10}$;
(3)若购买乒乓球门票顶点总款数站全部门票总款数的$\frac{3}{40}$,求每张乒乓球门票的价格.
 下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:
下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:(1)其中观看足球比赛的门票有50张,观看乒乓球比赛的门票占全部门票的20%;
(2)公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地完全相同且充分洗匀),问员工小华抽到男篮门票的概率是$\frac{3}{10}$;
| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | x |
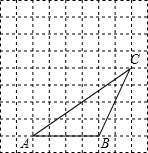 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.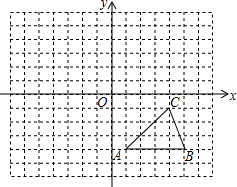 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,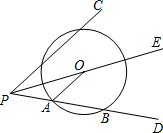 如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC.
如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC.