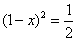题目内容
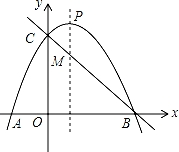
如图,抛物线y=ax2+bx+3经过A(﹣1,0),B(3,0)两点,且交y轴于点C,对称轴与抛物线相交于点P、与直线BC相交于点M.
(1)求该抛物线的解析式.
(2)在抛物线上是否存在一点N,使得|MN﹣ON|的值最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(3)连接PB,请探究:在抛物线上是否存在一点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)根据待定系数法,可得函数解析式;
(2)根据三角形两边之和大于第三边,可得N在直线OM上,根据解方程组,可得答案;
(3)根据平行线间的距离相等,可得过P点平行BC的直线,根据解方程组,可得Q点坐标,再根据BC向下平移BC与l1相距的单位,可得l2,根据解方程组,可得答案.
【解答】解:(1)将A、B两点代入解析式,得
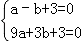 ,
,
解得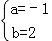 .
.
故抛物线的解析式为y=﹣x2+2x+3
(2)存在点N使得|MN﹣ON|的值最大.过程如下:
如图1:
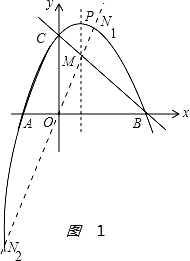
作直线OM交抛物线于两点,则两交点即为N点,
y=﹣x2+2x+3的对称轴为x=1.
设BC的解析式为y=kx+b,将B(3,0),C(0,3)代入函数解析式,得
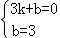 ,解得
,解得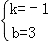 ,
,
BC的解析式为y=﹣x+3,
当x=1时,y=2,即M(1,2).
设直线OM的解析式为y=kx,将M(1,2)代入函数解析式,得
k=2.
直线OM的解析式为y=2x.
联立抛物线与直线OM的解析式,可得
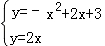
解得: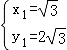 ,
,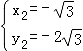
∴存在点N,其坐标为N1(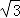 ,2
,2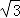 ),N2(﹣
),N2(﹣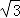 ,﹣2
,﹣2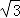 )
)
(3)如图2:
 ,
,
由题意可得:P(1,4),直线BC的解析式为y=﹣x+3
∵S△QMB=S△PMB,
∴点Q在过点P且平行于BC的直线l1上,设其交点为Q1;或在BC的下方且平行于BC的直线l2上,设其交点为Q2,Q3,
∴设l1的解析式为y=﹣x+b
把点P的坐标代入可得:b=5
∴设l1的解析式为y=﹣x+5
联立得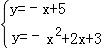
解得: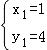 (不符合题意,舍),
(不符合题意,舍), ,
,
∴Q1(2,3).
根据对称性可求得直线l2的解析式为y=﹣x+1
联立得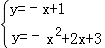
解得 ,
,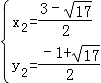
∴Q2( ,
,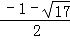 ),Q3(
),Q3(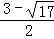 ,
,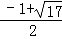 ),
),
综上所述,满足条件的点Q共有3个,其坐标分别为Q1(2,3),Q2( ,
,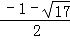 ),Q3(
),Q3(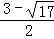 ,
,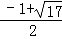 ).
).
【点评】本题考查了二次函数综合题,利用待定系数求函数解析式;利用同一条直线上两线段的差最大得出N在直线OM上是解题关键;利用平行线间的距离相等得出Q在过P点平行于BC的直线上是解题关键,注意BC下方距的距离是BC与l1相距的单位l2上存在符合条件的点,以防遗漏.

 名校课堂系列答案
名校课堂系列答案如图,已知抛物线y=﹣ax2+2ax+3a(a≠0)与x轴交于A、B两点,与y轴交于点C.
(1)请直接写出A、B两点的坐标.
(2)当a=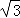 ,设直线AC与抛物线的对称轴交于点P,请求出△ABP的面积.
,设直线AC与抛物线的对称轴交于点P,请求出△ABP的面积.
情境:
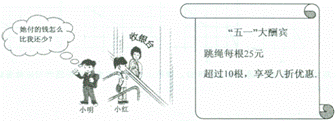 |
试根据图中的信息,解答下列问题:
(1)购买6根跳绳需付 元,购买12根跳绳需付 元;
(2)小红比小明多买2根,付款时小红反而比小明少5元.你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
 时该代数式的值.
时该代数式的值.
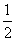 ,已知两次降价的百分率均为
,已知两次降价的百分率均为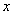 ,则列出方程正确的是( ).
,则列出方程正确的是( ). B.
B.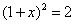 C.
C. 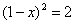 D.
D.