题目内容
6．平移边长为1的小菱形◇可以得到美丽的“中国结”图案，下面四个图案是由◇平移后得到的类似“中国结”的图案，其中第（1）个图形含边长为1的菱形2个，第（2）个图形含边长为1的菱形8个，第（3）个图形含边长为1的菱形18个，则第（6）个图形中含边长为1的菱形的个数是（ ）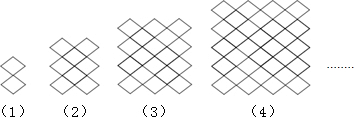
| A． | 32 | B． | 36 | C． | 50 | D． | 72 |
分析 认真审题，根据第（1）（2）（3）个图形所含有的小菱形的个数可以得到规律，即第（n）个图形含有小菱形2{n2n2个，再将n=6代入，即可得解．
解答 解：第（1）个图形：2=2=2×12；
第（2）个图形：8=2×4=2×22；
第（3）个图形：18=2×9=2×32；
…
第（n）个图形为2n2个，
∴第（6）个图形含有小菱形的个数为：2×62=72（个），
应选D．
点评 本题主要考查了图形的变化规律类的问题，认真审题，根据图形以及数字之间的关系找出变化的一般规律是解题的关键，注意认真总结．
练习册系列答案
相关题目
16．如果四个线段3，x，5，y的长度满足$\frac{3}{x}=\frac{5}{y}$，那么下列各式中不成立的一定是（ ）
| A． | $\frac{x}{y}=\frac{3}{5}$ | B． | $\frac{3+x}{x}=\frac{5+y}{y}$ | C． | $\frac{x}{y}=\frac{5}{3}$ | D． | $\frac{x-3}{3}=\frac{y-5}{5}$ |
17．下列各式中计算正确的是（ ）
| A． | （2x-y）2=4x2+y2-2xy | B． | （a2+2b）2=a2+4a2b+4b2 | ||
| C． | （a-b）2=a2-b2 | D． | （$\frac{1}{2}$x+3）2=$\frac{1}{4}$x2+3x+9 |
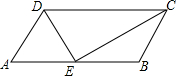已知，如图，在平行四边形ABCD中，AB=2AD，E为AB的中点，连接DE，EC，求证：DE⊥EC．