题目内容
18.(1)请先将下式化简,再选择一个适当的数代入求值.(1-$\frac{2}{x+2}$)-$\frac{1}{{x}^{2}-4}$÷$\frac{1}{{x}^{2}-4x+4}$.(2)解方程:$\frac{14}{x+8}$=$\frac{4}{x}$+$\frac{10}{3x+24}$.
分析 (1)根据分式的混合运算顺序和法则即可得出结果;注意因式分解;
(2)把分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)(1-$\frac{2}{x+2}$)-$\frac{1}{{x}^{2}-4}$÷$\frac{1}{{x}^{2}-4x+4}$
=$\frac{x}{x+2}$-$\frac{1}{(x-2)(x+2)}$×$\frac{(x-2)^{2}}{1}$
=$\frac{x}{x+2}$-$\frac{x-2}{x+2}$
=$\frac{2}{x+2}$
(2)去分母得:42x=12x+96+10x,
移项合并得:20x=96,
解得:x=4.8,
经检验x=4.8是分式方程的解;
因此,原方程的解为x=4.8.
点评 此题考查了分式方程的解法和分式的混合运算以及化简;解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
8.抛物线y=2(x+1)2-3的对称轴是( )
| A. | 直线x=1 | B. | 直线x=3 | C. | 直线x=-1 | D. | 直线x=-3 |
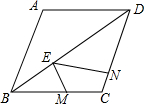 已知,如图,菱形ABCD中,∠ABC=60°,E为线段DB上的一点,∠MEN=60°,点M,N分别在直线BC,DC上.
已知,如图,菱形ABCD中,∠ABC=60°,E为线段DB上的一点,∠MEN=60°,点M,N分别在直线BC,DC上.